P3435 [POI2006]OKR-Periods of Words

传送门

KMP

对于这种一个字符串的问题

肯定先考虑KMP

如果一个串A要成为周期

设A长度为len_A，原串长度为len

那么串A要成为周期的充分必要条件就是：

从0 ~ (len-len_A)的串就要等于(len_A) ~ len的串

如下图：

 

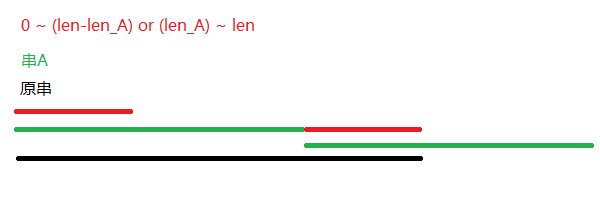
要怎么找出我们上图红色的串呢？

考虑 KMP 的 fail 数组

显然从 0 ~ fail[ len ] 的串是等于 len-fail[ len ] ~ len 的串的

所以这就是其中一个符合条件的串

但是不一定是最短的串（显然此串越短，周期越长）

怎么找最短的串也很简单：

不停的跳 fail[k] 直到 fail[k] 为 0

显然 0~k 就是最短的串

放个图有助于理解：

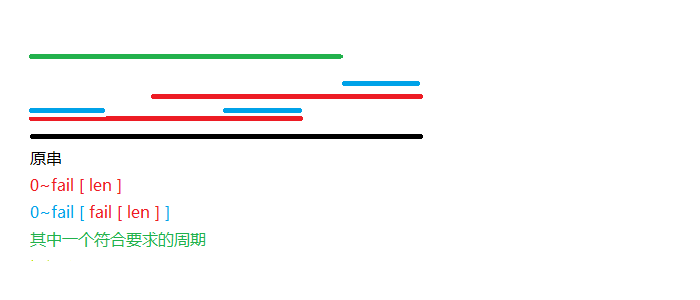
但是这样复杂度会卡到 $O(n^2)$，把 $fail$ 路径压缩一下就行了

代码很好写，注意 $long\ long$：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int N=1e6+7;
int n,fail[N];
long long ans;
char s[N];
int main()
{
    cin>>n;
    scanf("%s",s);
    int k=0;
    for(int i=1;i<n;i++)
    {
        while(k&&s[i]!=s[k]) k=fail[k];
        fail[i+1]= s[i]==s[k] ? ++k : 0;
    }
    for(int i=1;i<=n;i++)
    {
        k=i;
        while(fail[k]) k=fail[k];
        if(fail[i]) fail[i]=k;
        ans+=(i-k);
    }
    cout<<ans;
    return 0;
}