P2233 [HNOI2002]公交车路线

传送门

显然可以DP

设 f [ i ] [ j ] 表示已经换了 i 次车，现在在 j 号车站（j = 1~8 分别表示A~H）时的方案数

那么 f [ i ] [ j ] = f [ i-1 ] [ j-1 ] + f [ i-1 ] [ j+1 ]

注意一下当 j=1 和 j=8 时的情况

还要注意状态不能从 j=5 转移过来（j=5 表示 E号车站，当到达E号车站时就不会再走了）

但是数据太大

考虑矩阵优化

每个转移都有了

那么构造一个矩阵P，使初始状态，显然为[ 1,0,0,0,0,0,0,0]

（一开始肯定只有在A号车站有一种方案）

乘上 n 个P可以变成最终状态

在纸上画一画很快就可以得到一个 8 * 8 的矩阵：

 

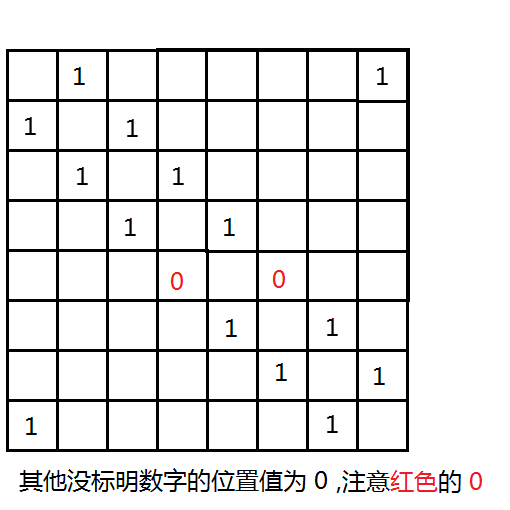
然后就可以了

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
const int mo=1000;
struct matrix
{
    int a[9][9];
    matrix() { memset(a,0,sizeof(a)); }
    matrix operator * (matrix &tmp)
    {
        matrix c;
        for(int i=1;i<=8;i++)
            for(int j=1;j<=8;j++)
                for(int k=1;k<=8;k++)
                    c.a[i][j]=(c.a[i][j]+(a[i][k]*tmp.a[k][j])%mo)%mo;
        return c;
    }
}b,p;
int n;
matrix ksm(matrix x,int y)
{
    matrix res;
    for(int i=1;i<=8;i++) res.a[i][i]=1;
    while(y)
    {
        if(y&1) res=(res*x);
        x=x*x;
        y>>=1;
    }
    return res;
}
int main()
{
    cin>>n;
    b.a[1][1]=1;
    p.a[2][1]=p.a[8][1]=1;
    p.a[1][2]=p.a[3][2]=1;
    p.a[2][3]=p.a[4][3]=1;
    p.a[3][4]=1;
    p.a[4][5]=p.a[6][5]=1;
    p.a[7][6]=1;
    p.a[6][7]=p.a[8][7]=1;
    p.a[1][8]=p.a[7][8]=1;
    p=ksm(p,n);
    b=b*p;
    printf("%d",b.a[1][5]);
    return 0;
}