[SDOI2009]Elaxia的路线
现在看看自己早期的题解真是惨不忍睹...(upd in 2019.8.11)
算法 最短路+DAG上的dp+建图
思路
首先是求最短路,但是题目没给出边的范围,所以我选用 $Dijkstra$ 求最短路,SPFA可能会爆炸
先分别求出以两个人为起点的单源最短路径,然后判断一条边 $(a,b)$ 是否在最短路径上只要判断 $dis[a]+map[a][b]$ 是否等于 $dis[b]$
其中 $map[a][b]$ 表示从点a到点b的 直接 距离
貌似不用走四遍最短路..
找出最短路径(注意是路径不是路程)后用其中一个人的最短路径建一个图:
如果这个人的最短路径有一种方案使得路径经过 $(a,b)$ 就从 $a$ 连一条边到 $b$,显然这个图是 $DAG$,然后就可以考虑在 $DAG$ 上跑 $dp$ 了
具体就是对于新图的一边连接的两点 $a,b$,如果边 $(a,b)$ 同时在另一个人的最短路径上,那么 $f[b]=max(f[b],f[a]+map[a][b])$
其中 $f[i]$ 表示以 $i$ 为终点的连续的公共路径的最大长度,最后枚举每个点的 $f[i]$ 取 $max$ 就是答案了
顺便付上自己搞的的样例图
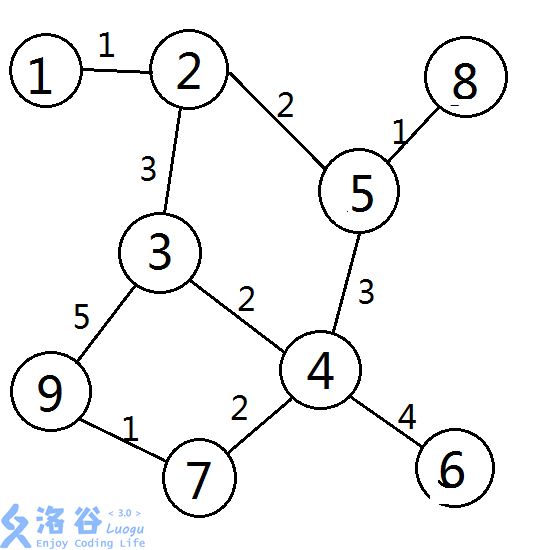
具体操作代码里注释还是挺细的吧,因为只要两遍最短路所以常数比较优秀 ?
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> #include<vector> #include<queue> using namespace std; inline int read() //顺手打一个快读 { int res=0; char ch=getchar(); while(ch>'9'||ch<'0') ch=getchar(); while(ch>='0'&&ch<='9') { res=res*10+ch-'0'; ch=getchar(); } return res; } struct node//为Dijkstra的优先队列开的结构体 { int u,v;//v存储节点编号,u存储到当时点v的最短路径 bool operator < (const node &b) const{ return u>b.u; }//重载运算符 }; priority_queue <node> q;//Dijkstra的优先队列 struct edge { int from,to; }e[5000005]; int fir[1505],cnt;//存边(边数可能较大,用链式前向星存边会比vector快一些) int map[1505][1505];//map[i][j]存从点i到点j的直接距离 inline void add(int a,int b,int c) { e[++cnt].from=fir[a]; fir[a]=cnt; e[cnt].to=b; map[a][b]=c; }//链式前向星加边 int xa,ya,xb,yb,n,m; int dis[1505][2]; //dis[i][0]存 Elaxia从xa到各点的距离,dis[i][1]存w**从xb到各点的距离 inline void dijk(int sta,int k)//Dijkstra求最短路 { dis[sta][k]=0; node p; p.u=0; p.v=sta; q.push(p); while(q.empty()==0) { int u=q.top().u,v=q.top().v; q.pop();//出队 if(u!=dis[v][k]) continue;//优化 for(int i=fir[v];i;i=e[i].from) { int to=e[i].to; if(dis[to][k]>dis[v][k]+map[v][to])//松弛操作 { dis[to][k]=dis[v][k]+map[v][to]; p.u=dis[to][k]; p.v=to; q.push(p);//入队 } } } } vector <int> v[1505];//懒得用链式前向星了,直接用vector存Elaxia的最短路线就好了 int f[1505],du[1505],ans; //f[i]表示以i为终点的最长连续 公共最短路长度,du[i]存入度 queue <int> qa; bool vis[1505],pd[1505][1505],p[1505]; //vis存Elaxia最短路线上的点 //pd[i][j]=1表示w**的最短路线中有经过从i到j的边,p是用来判断节点是否在队列qa中 inline void slove() { memset(dis,0x7f,sizeof(dis)); dijk(xa,0); dijk(xb,1); qa.push(ya); //反向找出最短路径上的点,保证先出队的节点在Elaxia的最短路径上处于更后的位置 //从终点开始找,保证找到的满足条件的点一定在Elaxia的最短路上 vis[ya]=1; while(qa.empty()==0) { int x=qa.front(); qa.pop(); for(int i=fir[x];i;i=e[i].from) { int u=e[i].to; if(dis[u][0]+map[u][x]==dis[x][0]) //如果一个节点u满足条件,说明u在Elaxia的最短路上 { v[u].push_back(x);//从u到点x连一条有向边 du[x]++;//点x的入度加一 if(vis[u]==0)//如果没有加入过 { qa.push(u);//把u加入队列,从而找到更"前面"的点 vis[u]=1;//现在加入过了 } } } } //此时qa已经空了,可以重复利用 qa.push(yb); //开始找w**的最短路径 p[yb]=1;//vis数组要留着,重新开一个数组p while(qa.empty()==0)//同上 { int x=qa.front(); qa.pop(); for(int i=fir[x];i;i=e[i].from) { int u=e[i].to; if(dis[u][1]+map[u][x]==dis[x][1])//同上 { pd[x][u]=pd[u][x]=1;//这次不用连边了,方便后面的判断 //正反都要判断,可能是反着走 if(p[u]==0) { p[u]=1; qa.push(u); } } } } //以下为DAG上的dp for(int i=1;i<=n;i++) if(du[i]==0&&vis[i])//如果i点入度为零且 Elaxia的最短路经过i qa.push(i);//把i加入qa while(qa.empty()==0) { int x=qa.front(); qa.pop(); int len=v[x].size(); for(int i=0;i<len;i++) { int u=v[x][i];//首先能够保证 Elaxia的最短路经过边x->i du[u]--;//入度减一 if(pd[x][u]) //如果边x->i也被w**的最短路经过 f[u]=max(f[u],f[x]+map[x][u]);//更新长度 if(du[u]==0) qa.push(u);//dp要按照拓扑序来保证这个点前面的所有点都访问过了 } } //以上为DAG上的dp for(int i=1;i<=n;i++) ans=max(ans,f[i]);//找出答案 } int main() { memset(map,0x7f,sizeof(map)); cin>>n>>m; cin>>xa>>ya>>xb>>yb; int a,b,c; for(int i=1;i<=m;i++) { a=read(); b=read(); c=read(); add(a,b,c); add(b,a,c); } slove(); cout<<ans; return 0;//简单易懂的主程序 }
然而洛谷的数据真的水..就过了
其实这是有问题的(感谢Brave_Cattle 巨佬指出错误)
有一种可能数据:
4 4
1 4 2 3
1 2 10
1 3 1
4 2 9
4 3 2
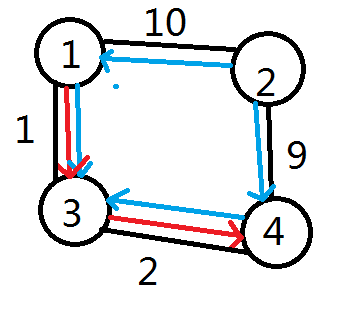
显然答案是 $2$,但是我的程序输出是$3$...
因为我没有考虑到最短路径只能选一种走...
那要怎么解决呢
也不难,虽然要考虑正反方向,但是显然不会一下正着走,一下反着走
所以分开讨论一下就好了..然后代码就变得更长了...
懒得重新写代码了...
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> #include<vector> #include<queue> using namespace std; inline int read() //顺手打一个快读 { int res=0; char ch=getchar(); while(ch>'9'||ch<'0') ch=getchar(); while(ch>='0'&&ch<='9') { res=res*10+ch-'0'; ch=getchar(); } return res; } struct node//为Dijkstra的优先队列开的结构体 { int u,v;//v存储节点编号,u存储到当时点v的最短路径 bool operator < (const node &b) const{ return u>b.u; }//重载运算符 }; priority_queue <node> q;//Dijkstra的优先队列 struct edge { int from,to; }e[5000005]; int fir[1505],cnt;//存边(边数可能较大,用链式前向星存边会比vector快一些) int map[1505][1505];//map[i][j]存从点i到点j的直接距离 inline void add(int a,int b,int c) { e[++cnt].from=fir[a]; fir[a]=cnt; e[cnt].to=b; map[a][b]=c; }//链式前向星加边 int xa,ya,xb,yb,n,m; int dis[1505][2]; //dis[i][0]存 Elaxia从xa到各点的距离,dis[i][1]存w**从xb到各点的距离 inline void dijk(int sta,int k)//Dijkstra求最短路 { dis[sta][k]=0; node p; p.u=0; p.v=sta; q.push(p); while(q.empty()==0) { int u=q.top().u,v=q.top().v; q.pop();//出队 if(u!=dis[v][k]) continue;//优化 for(int i=fir[v];i;i=e[i].from) { int to=e[i].to; if(dis[to][k]>dis[v][k]+map[v][to])//松弛操作 { dis[to][k]=dis[v][k]+map[v][to]; p.u=dis[to][k]; p.v=to; q.push(p);//入队 } } } } vector <int> v[1505];//懒得用链式前向星了,直接用vector存Elaxia的最短路线就好了 int f[1505],du[1505],ans; //f[i]表示以i为终点的最长连续 公共最短路长度,du[i]存入度 queue <int> qa; bool vis[1505],pd[1505][1505],p[1505]; //vis存Elaxia最短路线上的点 //pd[i][j]=1表示w**的最短路线中有经过从i到j的边,p是用来判断节点是否在队列qa中 int duu[1505];//du数组的拷贝 int t[2265025][2],tot; inline void slove() { memset(dis,0x7f,sizeof(dis)); dijk(xa,0); dijk(xb,1); qa.push(ya); //反向找出最短路径上的点,保证先出队的节点在Elaxia的最短路径上处于更后的位置 //从终点开始找,保证找到的满足条件的点一定在Elaxia的最短路上 vis[ya]=1; while(qa.empty()==0) { int x=qa.front(); qa.pop(); for(int i=fir[x];i;i=e[i].from) { int u=e[i].to; if(dis[u][0]+map[u][x]==dis[x][0]) //如果一个节点u满足条件,说明u在Elaxia的最短路上 { v[u].push_back(x);//从u到点x连一条有向边 du[x]++;//点x的入度加一 if(vis[u]==0)//如果没有加入过 { qa.push(u);//把u加入队列,从而找到更"前面"的点 vis[u]=1;//现在加入过了 } } } } //此时qa已经空了,可以重复利用 qa.push(yb); //开始找w**的最短路径 p[yb]=1;//vis数组要留着,重新开一个数组p while(qa.empty()==0)//同上 { int x=qa.front(); qa.pop(); for(int i=fir[x];i;i=e[i].from) { int u=e[i].to; if(dis[u][1]+map[u][x]==dis[x][1])//同上 { pd[u][x]=1;//这次不用连边了,方便后面的判断 t[++tot][0]=u; t[tot][1]=x; //可能路径方向相反,先用一个数组存着 if(p[u]==0) { p[u]=1; qa.push(u); } } } } //以下为DAG上的dp //第一遍先找方向相同的路径 for(int i=1;i<=n;i++) { if(du[i]==0&&vis[i])//如果i点入度为零且 Elaxia的最短路经过i qa.push(i);//把i加入qa duu[i]=du[i];//拷贝一下du,因为要用两次 } while(qa.empty()==0) { int x=qa.front(); qa.pop(); int len=v[x].size(); for(int i=0;i<len;i++) { int u=v[x][i];//首先能够保证 Elaxia的最短路经过边x->v[x][i] duu[u]--;//入度减一 if(pd[x][u]) //如果边x->i也被w**的最短路经过 f[u]=max(f[u],f[x]+map[x][u]);//更新长度 if(duu[u]==0) qa.push(u);//dp要按照拓扑序来保证这个点前面的所有点都访问过了 } } for(int i=1;i<=n;i++) ans=max(ans,f[i]);//更新答案 //第二遍找方向相反的路径,同上 memset(f,0,sizeof(f)); for(int i=1;i<=tot;i++) { pd[t[i][0]][t[i][1]]=0; pd[t[i][1]][t[i][0]]=1; //把路径换个方向 } for(int i=1;i<=n;i++) if(du[i]==0&&vis[i]) qa.push(i);//同上 while(qa.empty()==0) { int x=qa.front(); qa.pop(); int len=v[x].size(); for(int i=0;i<len;i++) { int u=v[x][i]; du[u]--; if(pd[x][u]) f[u]=max(f[u],f[x]+map[x][u]); if(du[u]==0) qa.push(u); } }//同上 //以上为DAG上的dp for(int i=1;i<=n;i++) ans=max(ans,f[i]); } int main() { memset(map,0x7f,sizeof(map)); cin>>n>>m; cin>>xa>>ya>>xb>>yb; int a,b,c; for(int i=1;i<=m;i++) { a=read(); b=read(); c=read(); add(a,b,c); add(b,a,c); } slove(); cout<<ans; return 0;//简单易懂的主程序 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号