P3748 [六省联考2017]摧毁“树状图”
显然是可以树形 $dp$ 的
对每个节点维护以下 $5$ 个东西
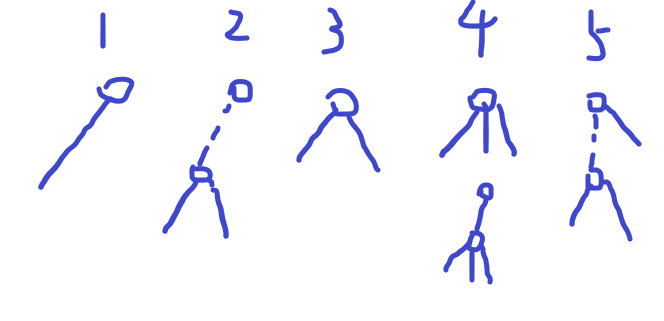
$1.$ 从当前节点出发往下的链的最大贡献
$2.$ 节点子树内不经过本身的路径最大贡献
$3.$ 节点子树内经过本身的路径的最大贡献
$4.$ 从当前节点出发的一条链加上经过这条链的路径构成的图形的最大贡献
$5.$ 从当前节点出发的一条链加上不经过这条链的路径构成的图形的最大贡献
然后就可以大力讨论转移,算答案的时候也同样大力讨论,细节过多,过于恶心
注意上面那些东西的贡献都只考虑在子树内,如果当前节点不是根那么对答案的贡献还要考虑父亲的那一个联通块
代码里面的转移方程有注释(这个题真是丧心病狂)
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #include<vector> using namespace std; typedef long long ll; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } const int N=5e5+7; int T,G,n; vector <int> V[N]; int f[N][6],Ans; inline void Max(int &x,int y) { if(y>x) x=y; } void dfs(int x,int fa) { int fg= (!fa) ? 0 : 1,sz=V[x].size(); //fg 判断是否有父亲 int fr,sc,ti,fu,vfr,vsc,Lfr,Lsc,mx; //分别是:最长链,次长链,次次长链,次次次长链,最长链从哪个儿子贡献来的,次长链从哪个儿子贡献来的 //之前所有儿子贡献的最长路径,次长路径,之前儿子内部路径的最大贡献 //为了方便区分,链就是指从x本身出发的一条路径,路径是指不一定从x出发的路径,并且这里的"长"指的是贡献大 fr=sc=ti=fu=vfr=vsc=Lfr=Lsc=mx=0; for(int i=0;i<sz;i++) { int &v=V[x][i]; if(v==fa) continue; dfs(v,x); Max(f[x][0], f[v][0] + sz-1 - fg ); // 从儿子v贡献的链,sz-1是因为v本身的联通块没有贡献,-fg是不考虑父亲的贡献 Max(f[x][1], max(f[v][1],f[v][2]) ); // 意义显然 Max(f[x][3], f[v][3] + sz-1 - fg ); // 从儿子图形的尾巴延长一个节点 Max(f[x][4], f[v][4] + sz-1 - fg ); // 从儿子图形的链往上延长一个节点 Max(f[x][4], f[v][1] + sz - fg ); // 从不经过儿子的路径加上x本身一个节点作为链,sz不用减1因为儿子的联通块有贡献 Max(f[x][4], f[v][1] + fr + sz-1 - fg ); // 从不经过当前儿子的路径加上之前儿子的链延长一个节点 Max(f[x][4], f[v][2] + sz-1 - fg ); // 这一行和下一行 与 上一行和上上一行差不多意思,只是路径经过了当前儿子 Max(f[x][4], f[v][2] + fr + sz-2 - fg ); Max(f[x][4], f[v][0] + mx + sz-1 - fg ); // 最后别忘了当前儿子的链加上之前儿子路径的最大贡献 if(f[v][0]>=fr) { fu=ti, ti=sc, sc=fr, fr=f[v][0]; vsc=vfr, vfr=v; } else if(f[v][0]>=sc) fu=ti, ti=sc, sc=f[v][0], vsc=v; else if(f[v][0]>=ti) fu=ti,ti=f[v][0]; else Max(fu,f[v][0]); //以上维护前4的链 int tmp=max(f[v][1],f[v][2]); if(tmp>=Lfr) Lsc=Lfr,Lfr=tmp; else Max(Lsc,tmp); //以上维护前2的路径 Max(mx, max(f[v][1],f[v][2]-1) );//维护mx,注意f[v][2]要减1,因为此时v本身没有贡献 } Max(f[x][0],sz-fg); /*本身一个节点作为链*/ f[x][2]=f[x][0]; // 显然 f[x][2] 包括 f[x][0] 的情况 Max(f[x][2], fr + sc + sz-2 - fg ); // 当然也可以是最长链+次长链的贡献,sz-2是因为贡献最长链和次长链的儿子没有贡献联通块数量 Max(f[x][3], max(f[x][0],f[x][2]) ); // 显然 f[x][3] 包括 f[x][0] 和 f[x][2] 的情况 Max(f[x][3], fr + sc + ti + sz-3 - fg ); // 当前也可以是前 3 名的链的贡献 Max(Ans, Lfr + Lsc +1 ); // 答案可以是不相交的两条路径 Max(Ans,f[x][0] + fg); Max(Ans, max(f[x][2],f[x][3]) + fg ); // 也要考虑 0,2,3 图形的贡献,记得+fg Max(Ans, fr + sc + ti + fu + sz-4 ); // 还可以是前 4 名的链的贡献 for(int i=0;i<sz;i++) { int &v=V[x][i],one,two;//one是不经过当前儿子的最长链,two的不经过当前儿子的最长路径 if(v==fa) continue; if(v==vfr) one=sc,two=sc+ti; else if(v==vsc) one=fr,two=fr+ti; else one=fr,two=fr+sc; Max(Ans, f[v][1] + sz ); // Ans可以是儿子的路径加上 x 本身看成一条链 Max(Ans, f[v][1] + one + sz-1 ); // 可以是儿子子树内不经过v的路径加上 x 往下的一条链 Max(Ans, f[v][1] + two + sz-2 ); // 可以是儿子子树内不经过v路径加上经过 x 并且不经过当前儿子的路径 Max(Ans, f[v][2] + one + sz-2 ); // 同样要考虑儿子子树内经过 v 的路径加上一些东西 Max(Ans, f[v][2] + two + sz-3 ); Max(Ans, f[v][3] + sz-1 ); // 也可以是儿子的 3 图形往上加上 x 本身构成的图形的贡献 Max(Ans, f[v][3] + one + sz-2 ); // 也可以是儿子的 3 图形往上加上 x 往其他儿子的链构成的图形的贡献 Max(Ans, f[v][4] + sz-1 ); // 也可以是儿子的 4 图形往上加上 x 本身构成的图形的贡献 Max(Ans, f[v][4] + one + sz-2 ); // 也可以是儿子的 4 图形往上加上 x 往其他儿子的链构成的图形的贡献 } } inline void Clear() { Ans=0; for(int i=1;i<=n;i++) memset(f[i],0,sizeof(f[i])),V[i].clear(); } inline void solve() { n=read(); for(int i=1;i<=G;i++) int a=read(); for(int i=1;i<n;i++) { int a=read(),b=read(); V[a].push_back(b); V[b].push_back(a); } if(n==1) printf("0\n"); else dfs(1,0),printf("%d\n",Ans); } int main() { T=read(); G=read()<<1; while(T--) solve(),Clear(); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号