P3190 [HNOI2007]神奇游乐园
第一道插头 $dp$
由于讲不清楚所以假装各位早就会插头 $dp$ 了
首先要的是一个闭合回路，所以可以用括号表示法表示状态，然后大力分类讨论
$1.$ 没有右插头和下插头
那么我们可以啥也不干，或者加一个右插头和下插头
$2.$ 只有下插头没有右插头
那么我们可以要把下插头继续延伸，可以向下或者向右
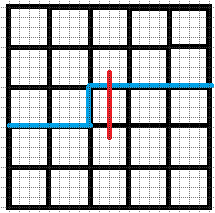
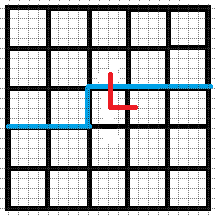
$3.$ 只有右插头没有下插头：
同理我们可以往下或者往右延伸
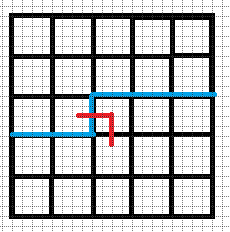
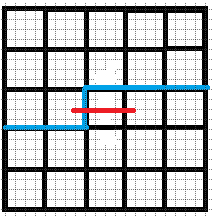
$4.$ 右插头和下插头都有：这个又要分情况讨论
$a.$ 插头都是左括号，那么要把两个联通还要把右边原来匹配的右括号改成左括号
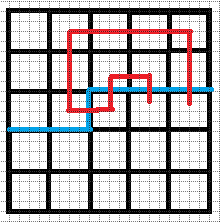
$b.$ 插头都是右括号，那么要把两个联通还要把左边原本匹配的左括号改成右括号
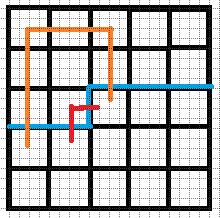
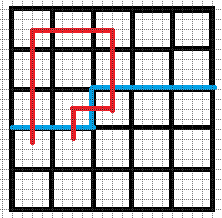
$c.$ 右插头是左括号，下插头是右括号，那么直接联通即可，不需要改变其他括号
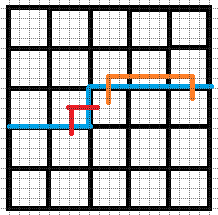
$d.$ 右插头是右括号，下插头是左括号，如果联通则一定形成一个闭合回路，那么如果其他地方没有插头则直接把当前状态计入答案，否则此状态不合法，不用延伸状态（右图是一种不合法状态）
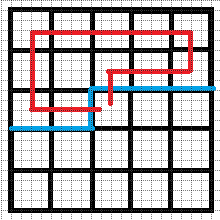
然后根据考虑到的所有状态慢慢转移即可......
因为数据比较大所以用滚动数组和哈希表维护状态，状态在加入哈希表时更新
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; typedef long long ll; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } const int N=3e5; const ll INF=1e18; int n,m,a[107][107],bit[17],cur,pre; ll f[2][N+7],Ans=-INF; int fir[N+7],from[N+7],to[2][N+7],cntt[2];//哈希表 inline void insert(int sta,ll val)//插入状态并更新f { int p=sta%N; for(int i=fir[p];i;i=from[i]) { if(to[cur][i]!=sta) continue; f[cur][i]=max(f[cur][i],val); return; } from[++cntt[cur]]=fir[p]; fir[p]=cntt[cur]; to[cur][cntt[cur]]=sta; f[cur][cntt[cur]]=val; } void DP() { cntt[cur]=1; int now,down,right; ll val; for(int i=1;i<=n;i++)//枚举行 { for(int j=1;j<=cntt[cur];j++) to[cur][j]<<=2;//每一行末尾,状态统一左移四进制下的一位 for(int j=1;j<=m;j++)//枚举列 { pre=cur; cur^=1; cntt[cur]=0; memset(fir,0,sizeof(fir));//清空哈希表 for(int k=1;k<=cntt[pre];k++)//枚举上一行的状态 { now=to[pre][k]; val=f[pre][k]; right=(now>>bit[j-1])%4; down=(now>>bit[j])%4;//提出插头状态 if(!down&&!right)//没有插头 { insert(now,val);//继续没有插头 if(j!=m) insert(now+(1<<bit[j-1])+((1<<bit[j])<<1),val+a[i][j]);//多一个右插头和下插头 } if(down&&!right)//只有下插头 { insert(now-down*(1<<bit[j])+down*(1<<bit[j-1]),val+a[i][j]);//向下延伸 if(j!=m) insert(now,val+a[i][j]);//向右延伸 } if(!down&&right)//只有右插头 { insert(now,val+a[i][j]);//向下延伸 if(j!=m) insert(now-right*(1<<bit[j-1])+right*(1<<bit[j]),val+a[i][j]);//向右延伸 } if(down==1&&right==1)//插头为'((' { int cnt=1; for(int l=j+1;l<=m;l++)//找到右边第一个和当前下插头匹配的')' { if((now>>bit[l])%4==1) cnt++; if((now>>bit[l])%4==2) cnt--; if(!cnt) { insert(now-(1<<bit[l])-(1<<bit[j-1])-(1<<bit[j]),val+a[i][j]);//联通并改')'为'(' break; } } } if(down==2&&right==2)//插头为'))' { int cnt=1; for(int l=j-2;l>=0;l--)//找到左边第一个和当前右插头匹配的'(' { if((now>>bit[l])%4==1) cnt--; if((now>>bit[l])%4==2) cnt++; if(!cnt) { insert(now+(1<<bit[l])-((1<<bit[j-1])<<1)-((1<<bit[j])<<1),val+a[i][j]);//联通并改'('为')' break; } } } if(down==1&&right==2)//')(' insert(now-((1<<bit[j-1])<<1)-(1<<bit[j]),val+a[i][j]);//直接联通即可 if(down==2&&right==1)//'()' if(now==((1<<bit[j])<<1)+(1<<bit[j-1]))//当前状态只有这两个插头 Ans=max(Ans,val+a[i][j]);//统计答案 } } } } int main() { n=read(),m=read(); for(int i=1;i<=10;i++) bit[i]=(i<<1); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]=read(); DP(); printf("%lld\n",Ans); return 0; }
