P1099 树网的核

传送门

BZOJ 上有加强版的数据 :$n<=10^6$，传送门

题面有点长...

考虑先把树的直径求出来，然后瞎搞一下

考虑直径上的点对答案的贡献，显然两个端点的贡献是最大的，可以直接在直径上用一个双指针维护一下左右边界 $l,r$，每次 $r$ 向右走，然后 $l$ 跟着走，贪心地想，显然 $l$ 能不走就不走是最优的

这样就可以尽可能地覆盖直径，使直径两端对答案贡献尽可能小了

然后考虑非直径的点的贡献，可以发现非直径的点对答案的贡献最多就是它到直径的距离，这样直接枚举所有直径点然后往非直径点 $dfs$ 求最大深度就行了

那如果此直径点没有被选择对答案有影响吗？

没有，因为它的贡献不会大于之前计算的直径两端点的贡献，看图理解（横着的一条路径是直径）：

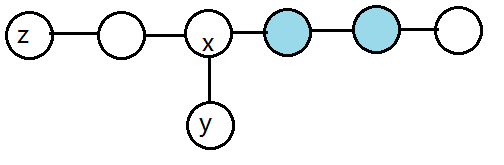
显然 $y$ 到 $x$ 距离一定不会大于 $z$ 到 $x$ 的距离，不然直径就不是横着的这条了

所以对答案的贡献显然 $z$ 会更大些

所以可以直接取 $max$

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
    return x*f;
}
const int N=5e5+7;
int fir[N],from[N<<1],to[N<<1],val[N<<1],cnt;
inline void add(int &a,int &b,int &c)
{
    from[++cnt]=fir[a];
    fir[a]=cnt; to[cnt]=b; val[cnt]=c;
}
int dis[N],fa[N];//dis是到根的距离，fa是父亲
int k;//最深点编号
bool p[N];//是否是直径端点
void dfs(int x,int f)//dfs求最深节点的编号和dis
{
    fa[x]=f;
    if(dis[x]>dis[k]) k=x;
    for(int i=fir[x];i;i=from[i])
    {
        int &v=to[i]; if(v==f||p[v]) continue;//注意不走直径
        dis[v]=dis[x]+val[i]; dfs(v,x);
    }
}
int n,s,rt,ans=1e9+7;
int main()
{
    int a,b,c;
    n=read(); s=read();
    for(int i=1;i<n;i++)
    {
        a=read(); b=read(); c=read();
        add(a,b,c); add(b,a,c);
    }
    k=1; dfs(k,0);//找到直径的一个端点
    rt=k; dis[rt]=0; dfs(k,0);//找到另一个端点
    for(int l=k,r=k;l;l=fa[l])
    {
        while(dis[r]-dis[l]>s) r=fa[r];//尺取法动态维护左右边界
        ans=min(ans, max(dis[l],dis[k]-dis[r]) );
    }
    for(int i=k;i;i=fa[i]) p[i]=1;//标记直径节点
    for(int i=k;i;i=fa[i])
    {
        k=i; dis[i]=0;
        dfs(i,fa[i]);//求每个非直径节点到直径的距离
        //可以发现此处的dfs不会更新k
    }
    for(int i=1;i<=n;i++) ans=max(ans,dis[i]);//取max
    printf("%d",ans);
    return 0;
}