对于最小割的进一步理解

以前只知道最小割就是最大流...网络流背个模板，没了

根本没有深入理解，最近写了一些题才知道自己很 $naive$

废话不多说，开始正题（假设大家都会网络流的代码，并且知道网络流在做什么）

首先最小割就是最大流（废话）

一条图的最小割中，一定有一些边，它们是满流的（如果不满流就不是最大流了）

不妨把这些边称作割边，显然，这些割边把图分成两个部分，一个与源点 $S$ 在同一个部分，一个与汇点 $T$在同一个部分

放图理解：

　　首先原图长这样：

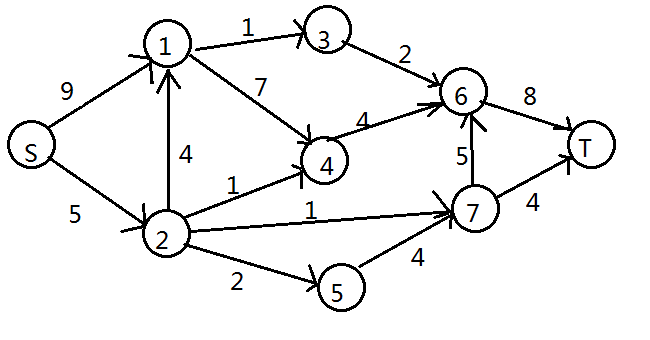
　　然后一种最小割长这样（红色的是满流的边）：

　

我们把与 $S$ 在同一个部分的点集叫作 $S$割，与 $T$ 在同一个部分的点集叫作 $T$割

那么 $S$割 包括点 ${1,2,4}$， $T$割 包括点 ${3,5,6,7}$

注意满流边不一定是割边，比如这个图：

 

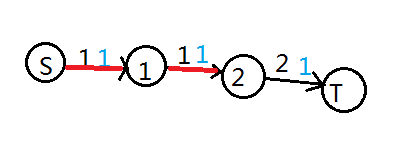
割边可以是 $(S,1)$ 或者是 $(1,2)$ ，显然对于这种有多解的最小割随便一种都合法

如果把边看成 $(u,v,cost)$（从 $u$ 到 $v$，花费（流量）是 $cost$ ），考虑最小割的实际意义

就是把点集分成 $S$割 和 $T$割 的最小花费

（请先好好理解以上理论再看下去$qwq$）

 

接下来考虑最小割模型中的三种边：

1. $(S,u,cost)$，意思是 如果 $u$ 在 $T$割（此边满流），那么要产生 $cost$ 的代价

2. $(u,T,cost)$，意思是 如果 $u$ 在 $S$割（此边满流），那么要产生 $cost$ 的代价

再进一步考虑一条边 $(u,v,cost)$ 的实际意义：如果把 $u$ 给 $S$割， $v$ 给 $T$割（此边满流），那么会产生 $cost$ 的代价

扩展一下，对于一条边 $(u,v,cost)$ ，如果 $cost$ 是正无穷 那么这个边的意思是什么？

光速回答，$u$ 和 $v$ 不能在同一个割集！

好像很有道理，因为这个边不可能满流，所以 $u$，$v$ 必须在同一个割集里

但是注意，边是有向边，从 $u$ 到 $v$！如果 $u$ 在 $T$割，$v$ 在 $S$割 也是合法的

所以这条边的真正意思是 ，如果 $u$ 在 $S$割，那么 $v$必须在 $S$割

（休息一下，一定要真正理解边的意义$qwq$）

 

更近一步，对于一种题型：有 $n$ 个点，每个点有一个价值 $val$ （可能为负），点之间有一些限制关系 $(x,y)$（选了点 $x$ 必须选点 $y$），并且保证对于任意限制 $(x,y)$， $val[x]>0,val[y]<0$，求获得的最大价值

显然最大价值相当于总的正的价值减去 最小要失去的价值（有些正点不能选，有些负点要选），考虑求出最小要失去的价值

构建网络流模型，把点 $u$ 给 $S$割 表示选择点 $u$，给 $T$割 说明不选点 $u$

对于一个限制 $(x,y)$，连 $(S,x,val[x])$，此边为割边表示 $x$ 不在 $S$割，那么就相当于不选择 $x$，会失去 $val[x]$ 价值（对最小割产生 $val[x]$ 的贡献）

连 $(y,T,-val[y])$ ，此边为割边表示 $y$ 在 $S$ 割，相当于选择 $y$，会得到 $val[y]$ 的负的价值（对最小割产生 $-val[y]$ 的贡献）

连 $(x,y,INF)$ 表示如果 $x$ 在 $S$割，那么 $y$ 也在 $S$割（选 $x$ 必须选 $y$）

因为最终每个点都要确定选或者不选，所以必须要把点集分成 $S$割 和 $T$割

所以最小割就是最小要失去的价值

 

例题：太空飞行计划问题

 

把实验看成正点，仪器看成负点，然后限制关系就是限制关系，直接把上面的方法套进来就好了$qwq$

要输出具体方案，直接看看那些点在 $S$割就好了，（网络流就不用放代码了吧$qwq$，毕竟网络流考的是建模$qwq$）

 

另一题例题：最大获利（同样的方法，不用再解释了吧$qwq$）

 

用这种思想可以很容易地证明最大权闭合子图的正确性（比我在网上看的其他方法好多了$qwq$）