P4381 [IOI2008]Island

传送门

显然题目给的图构成一个基环树森林

对于每个基环树单独考虑，显然每个都走直径是最优的

考虑如何求出基环树的直径

把直径分为两种情况考虑，首先可以找出环

因为直径可能不在环边上，所以对每个环上节点的子树进行一遍 $dfs$，求出每个节点子树的直径

维护 $dis[x]$ 表示节点 $x$ 到叶子节点的最长路程，那么直径就是每个节点儿子的 $dis$ 中最大和次大的和

可以一遍循环动态维护最大和次大

直径也可能在环上

设环上两点 $x,y$ 的距离为 $d(x,y)$，那么就是求最大的 $dis[x]+dis[y]+d(x,y)$

这样复杂度是 $O(n^2)$，考虑优化

按照套路，考虑把环断成链：

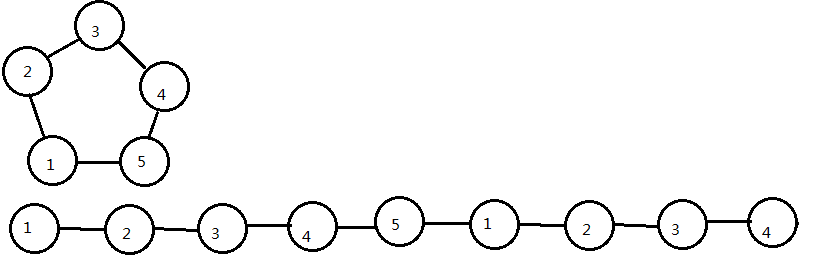
维护一条链上的距离前缀和 $sum[\ ]$，设 $y$ 在 $x$ 后面，那么就是求直径就是 $dis[x]+dis[y]+sum[y]-sum[x]$

换一下，就是求对于每一个 $y$，求链上区间 $x\in(y-n,y)$ 的 $(dis[x]-sum[x])$ 最大值 $+(dis[y]+sum[y])$（$n为环的节点数$）

显然这个东西我们可以单调队列优化

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
    return x*f;
}
const int N=1e6+7;
int fir[N],from[N<<1],to[N<<1],val[N<<1],cntt;
inline void add(int a,int b,int c)
{
    from[++cntt]=fir[a]; fir[a]=cntt;
    to[cntt]=b; val[cntt]=c;
}
struct edge{
    int v,w;//节点，边权
}To[N];//To存题目给出的数据
int n,tot,ring[N],d[N];//ring存环上节点，d存环上节点到下一环上节点的边的边权
ll ANS;
int fa[N];//存环节点的'父'节点
bool vis[N],p[N];//vis判断是否为走过的基环树节点,p判断是否是基环树环节点
void BFS(int x)//找环
{
    tot=0; vis[x]=1; int t;
    while(233)
    {
        t=To[x].v;
        if(vis[t])//找到就一路回跳并更新ring,d,p
        {
            ring[++tot]=t; d[tot]=To[t].w; p[t]=1;
            for(int i=x;i!=t;i=fa[i])
                p[i]=1,ring[++tot]=i,d[tot]=To[i].w;
            return;
        }
        vis[t]=1; fa[t]=x; x=t;//否则就继续找
    }
}
ll dis[N],res;//维护当前基环树直径
void dfs(int x,int f)//处理dis和子树直径最大值
{
    vis[x]=1;
    for(int i=fir[x];i;i=from[i])
    {
        int &v=to[i]; if(p[v]||v==f) continue;
        dfs(v,x); res=max(res,dis[x]+dis[v]+val[i]);
        //此时dis[x]还没有dis[v]+val[i]，所以res可以这样更新
        dis[x]=max(dis[x],dis[v]+val[i]);//更新dis
    }
}
int Q[N<<1]; ll sum[N<<1];
inline int id(int x) { return (x-1)%tot+1; }//把链节点换成环节点
inline ll calc(int x) { return dis[ring[id(x)]]-sum[x]; }
inline void solve()//单调队列
{
    int l=1,r=0;
    for(int i=1;i<=(tot<<1);i++)
    {
        sum[i]=sum[i-1]+d[id(i)];
        while(l<=r && i-Q[l]>=tot ) l++;
        if(l<=r) res=max(res,calc(Q[l])+sum[i]+dis[ring[id(i)]]);//先更新res
        while(l<=r && calc(i)>=calc(Q[r]) ) r--;//再更新队列
        Q[++r]=i;
    }
}
int main()
{
    n=read(); int a,b;
    for(int i=1;i<=n;i++)
    {
        a=read(),b=read();
        add(i,a,b); add(a,i,b);
        To[i].v=a; To[i].w=b;
    }
    for(int i=1;i<=n;i++)
    {
        if(vis[i]) continue;
        BFS(i); res=0;
        for(int j=1;j<=tot;j++) dfs(ring[j],0);
        solve(); ANS+=res;
    }
    printf("%lld",ANS);
    return 0;
}