P3979 遥远的国度

传送门

树剖模板，有换根操作

先打一个树剖模板

然后考虑换根有什么影响

对于两点间的路径上的询问显然没有影响

子树查询和更改有一些影响：

画个图，然后分类讨论一下

如果在原树上新根 $rt$ 不是询问的子树根 $x$ 的后代节点

那么不会有影响

否则，询问的区间就是整颗树减去 $rt$ 在原树上最高的是 $x$ 的儿子的祖先

画个图理解一下：

 

 

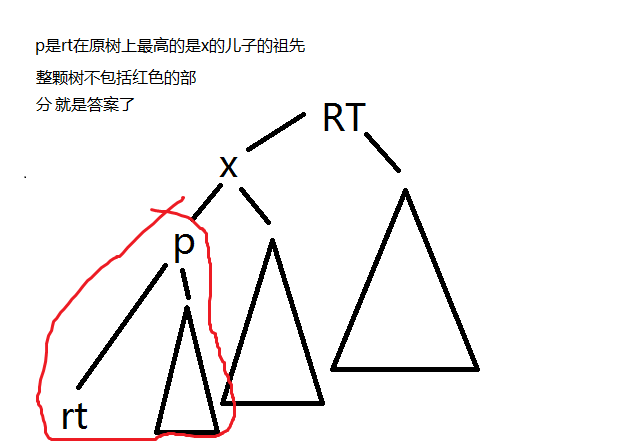
设节点 $p$ 在线段树上的位置为 $pos$，$p$在原树上的子树大小为 $sz$，那么答案就是

$max(query(1,pos-1)\ ,\ query(pos+sz,n))$

注意特判如果 $x$ 就是 $rt$ 那么就是询问整颗树

然后这题就完成了

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<vector>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
    return x*f;
}
const int N=2e5+7,INF=2147483647;
int fir[N],from[N<<1],to[N<<1],cntt;
inline void add(int &a,int &b)
{
    from[++cntt]=fir[a]; fir[a]=cntt;
    to[cntt]=b;
}
int n,m,rt,v[N];
int fa[N],dep[N],sz[N],son[N];
int f[N][21];
void dfs1(int x)
{
    for(int i=1;i<=20;i++) f[x][i]=f[f[x][i-1]][i-1];
    dep[x]=dep[fa[x]]+1; sz[x]=1;
    int mxsz=0;
    for(int i=fir[x];i;i=from[i])
    {
        int &v=to[i]; if(v==fa[x]) continue;
        fa[v]=f[v][0]=x; dfs1(v); sz[x]+=sz[v];
        if(sz[v]>mxsz) mxsz=sz[v],son[x]=v;
    }
}
int Top[N],id[N],val[N],cnt;
void dfs2(int x,int topp)
{
    id[x]=++cnt; val[cnt]=v[x]; Top[x]=topp;
    if(!son[x]) return;
    dfs2(son[x],topp);
    for(int i=fir[x];i;i=from[i])
    {
        int &v=to[i]; if(v==fa[x]||v==son[x]) continue;
        dfs2(v,v);
    }
}

int t[N<<2],vtag[N<<2];
bool tag[N<<2];
inline void pushdown(int o,int l,int r)
{
    if(!tag[o]) return;
    t[o]=vtag[o]; tag[o]=0;
    if(l==r) return;
    int lc=o<<1,rc=lc|1;
    tag[lc]=tag[rc]=1;
    vtag[lc]=vtag[rc]=vtag[o];
}
inline void pushup(int o) { t[o]=min(t[o<<1],t[o<<1|1]); }
int ql,qr,K,res;
void build(int o,int l,int r)
{
    if(l==r) { t[o]=val[l]; return; }
    int mid=l+r>>1;
    if(mid>=l) build(o<<1,l,mid);
    if(mid<r) build(o<<1|1,mid+1,r);
    pushup(o);
}
void change(int o,int l,int r)
{
    pushdown(o,l,r);
    if(l>qr||r<ql) return;
    if(l>=ql&&r<=qr) { vtag[o]=K,tag[o]=1; pushdown(o,l,r); return; }
    int mid=l+r>>1;
    change(o<<1,l,mid); change(o<<1|1,mid+1,r);
    pushup(o);
}
void query(int o,int l,int r)
{
    pushdown(o,l,r);
    if(l>qr||r<ql) return;
    if(l>=ql&&r<=qr) { res=min(res,t[o]); return; }
    int mid=l+r>>1;
    query(o<<1,l,mid); query(o<<1|1,mid+1,r);
    pushup(o);
}

inline int LCA(int x,int y)
{
    while(Top[x]!=Top[y])
    {
        if(dep[x]<dep[y]) swap(x,y);
        x=fa[Top[x]];
    }
    return dep[x]<dep[y] ? x : y;
}
inline void Change(int x,int y)
{
    while(Top[x]!=Top[y])
    {
        if(dep[Top[x]]<dep[Top[y]]) swap(x,y);
        ql=id[Top[x]]; qr=id[x]; change(1,1,n);
        x=fa[Top[x]];
    }
    if(dep[x]<dep[y]) swap(x,y);
    ql=id[y]; qr=id[x]; change(1,1,n);
}
inline int Query(int x)
{
    res=INF;
    if(x==rt) { ql=1,qr=n,query(1,1,n); return res; }
    if(LCA(x,rt)!=x)
    {
        ql=id[x]; qr=id[x]+sz[x]-1;
        query(1,1,n); return res;
    }
    int p=rt;
    for(int i=20;i>=0;i--) if(dep[f[p][i]]>dep[x]) p=f[p][i];
    ql=1; qr=id[p]-1; query(1,1,n);
    ql=id[p]+sz[p]; qr=n; query(1,1,n);
    return res;
}

int main()
{
    //freopen("a15.in","r",stdin);
    //freopen("data.out","w",stdout);
    n=read(),m=read(); int op,a,b;
    for(int i=1;i<n;i++)
    {
        a=read(),b=read();
        add(a,b); add(b,a);
    }
    for(int i=1;i<=n;i++) v[i]=read();
    rt=read();
    dfs1(rt); dfs2(rt,rt);
    build(1,1,n);
    while(m--)
    {
        op=read();
        if(op==1) rt=read();
        if(op==2)
        {
            a=read(),b=read(),K=read();
            Change(a,b);
        }
        if(op==3) printf("%d\n",Query(read()));
    }
    return 0;
}