P3233 [HNOI2014]世界树
看到指定的总节点数小于等于 300000 就知道要搞虚树了
考虑如何在虚树确定每个议事处控制的节点数量
可以两遍dfs
第一遍求儿子对父亲的影响,第二遍求父亲对儿子影响
注意搜索顺序,这样就可以把影响扩展到其他子树了
如图:
初始时只有本身被影响

经过第一遍dfs后父亲被影响:
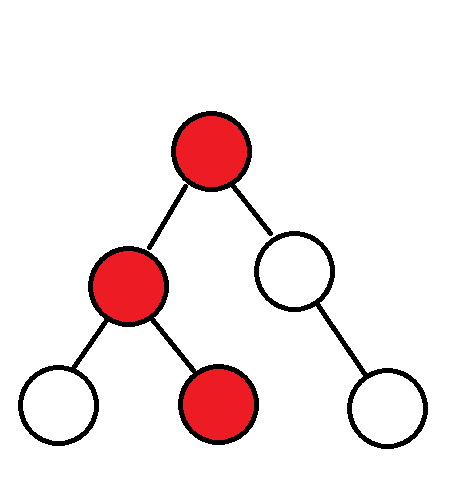
经过第二遍dfs后儿子被影响:

这样就可以考虑到所有情况了
然后对于虚树上的每一条边,考虑它的贡献
对于虚树上的一条边 $(u,v)$ ($u$ 是父节点,$u,v$被同一点控制),我们可以在原树上从$v$倍增跳到离$u$最近的节点$p_1$
那么设原树上的节点子树大小为 $sz$,那么虚树上那条边的贡献就是$sz[p_1]-sz[v]$
如果$u,v$不被同一点控制,那么中间肯定有一个分界点,我们也可以倍增从$v$在原树上跳到分界点$p_2$
设 $bel[x]$ 存节点 x 属于的节点
在$p_2$及以下的部分属于$bel[v]$,对$bel[v]的$贡献为 $sz[p_2]-sz[v]$
上面一直到 $u$ 的部分属于 $bel[u]$,贡献显然为 $sz[p_1]-sz[p_2]$
对于一个节点$x$,它还有一部分子树不在虚树上,设它们的数量为$sur[x]$,
初始时$sur[x]=sz[x]$,然后我们每次枚举一条虚树边就把$sur[x]$减去那条边的子树大小
($sur[x]=sur[x]-sz[p_1]$)
最后的$sur[x]$就是在$x$子树上但不在虚树上的节点数量了
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<cstring> #include<vector> using namespace std; typedef long long ll; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } const int N=3e5+7; int fir[N],from[N<<1],to[N<<1],cntt;//存原树 inline void add(int &a,int &b) { from[++cntt]=fir[a]; fir[a]=cntt; to[cntt]=b; } int n,m; int dep[N],sz[N],f[N][21],dfn[N],dfs_clock;//f是倍增数组 void dfs(int x)//预处理各种东西 { dep[x]=dep[f[x][0]]+1; sz[x]=1; dfn[x]=++dfs_clock; for(int i=1;i<=20;i++) f[x][i]=f[f[x][i-1]][i-1]; for(int i=fir[x];i;i=from[i]) { int v=to[i]; if(dfn[v]) continue; f[v][0]=x; dfs(v); sz[x]+=sz[v]; } } inline int LCA(int x,int y)//求LCA { if(dep[x]<dep[y]) swap(x,y); for(int i=20;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i]; if(x==y) return x; for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } int st[N<<1],Top; vector <int> v[N];//存虚树 inline void ins(int x)//插入一个节点到虚树里 { if(Top==1) { st[++Top]=x; return; } int lca=LCA(x,st[Top]); if(lca!=st[Top]) while(Top>1 && dfn[st[Top-1]]>=dfn[lca]) v[st[Top-1]].push_back(st[Top]),Top--; if(lca!=st[Top]) v[lca].push_back(st[Top]),st[Top]=lca; st[++Top]=x; } int cnt[N<<1],bel[N<<1],sur[N<<1]; //cnt存每个议事处控制的数量 bool pd[N];//pd判断是否是议事处 void dfs1(int x)//第一遍dfs考虑儿子对父亲的贡献 { int len=v[x].size(); sur[x]=sz[x]; if(pd[x]) bel[x]=x;//如果它本身是议事处,那么显然被自己控制 else bel[x]=0;//注意多组询问,要清0 for(int i=0;i<len;i++) { int t=v[x][i]; dfs1(t);//先向下dfs再考虑儿子的影响 if(!bel[x]) { bel[x]=bel[t]; continue; }//特判 int d1=dep[bel[t]]-dep[x],d2=dep[bel[x]]-dep[x]; if(d1<d2) bel[x]=bel[t];//考虑用儿子更新bel else if(d1==d2&&bel[t]<bel[x]) bel[x]=bel[t];//注意如果距离相同取编号小的 } } inline int dis(int x,int y) { return dep[x]+dep[y]-2*dep[LCA(x,y)]; }//求不在一条链上的两点距离 void dfs2(int x)//第二遍dfs考虑父亲对儿子的影响 { int len=v[x].size(); for(int i=0;i<len;i++) { int t=v[x][i],d1=dis(bel[x],t),d2=dis(bel[t],t); if(d1<d2) bel[t]=bel[x];//考虑用父亲更新儿子 else if(d1==d2&&bel[x]<bel[t]) bel[t]=bel[x];//距离相同取编号小的 dfs2(t);//注意此时先更新儿子再dfs } } void dp(int x)//最后dp统计贡献 { int len=v[x].size(),p1,p2,t; for(int i=0;i<len;i++) { p1=p2=t=v[x][i]; dp(t); for(int j=20;j>=0;j--) if(dep[f[p1][j]]>dep[x]) p1=f[p1][j];//倍增找到离x最近的节点 sur[x]-=sz[p1];//更新sur if(bel[x]==bel[t]) cnt[bel[x]]+=sz[p1]-sz[t];//如果边上两点属于同一议事处直接更新贡献 else { for(int j=20;j>=0;j--)//否则倍增找到分界点 { if(dep[f[p2][j]]<=dep[x]) continue; int d1=dis(f[p2][j],bel[t]),d2=dis(f[p2][j],bel[x]); if(d1<d2) p2=f[p2][j]; else if(d1==d2&&bel[t]<bel[x]) p2=f[p2][j];//同样如果距离一样取编号小的 } cnt[bel[x]]+=sz[p1]-sz[p2]; cnt[bel[t]]+=sz[p2]-sz[t];//两边都要更新 } } cnt[bel[x]]+=sur[x];//最后贡献再加上sur[x] v[x].clear();//记得清空 } inline bool cmp(const int &a,const int &b) { return dfn[a]<dfn[b]; }//按dfs序排序 int d[N],dd[N]; inline void solve()//处理询问 { int t=read(); for(int i=1;i<=t;i++) { d[i]=dd[i]=read(); pd[d[i]]=1; } sort(d+1,d+t+1,cmp); st[Top=1]=1; for(int i=(pd[1] ? 2 : 1);i<=t;i++) ins(d[i]);//插入 while(Top>1) v[st[Top-1]].push_back(st[Top]),Top--; dfs1(1); dfs2(1); dp(1); for(int i=1;i<=t;i++) { printf("%d ",cnt[dd[i]]); pd[dd[i]]=cnt[dd[i]]=0;//记得清空 } printf("\n"); } int main() { // freopen("data.in","r",stdin); // freopen("data.out","w",stdout); int a,b; n=read(); for(int i=1;i<n;i++) { a=read(),b=read(); add(a,b); add(b,a); } dfs(1); m=read(); while(m--) solve(); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号