BZOJ 1007: [HNOI2008]水平可见直线

传送门

自己在纸上画一下，发现最后留下的线段是下凹的，大概是这样：

 

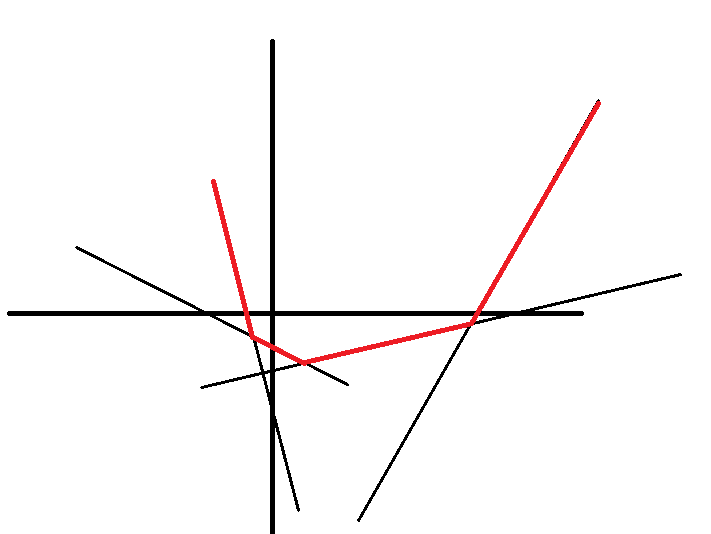
把所有直线按斜率从小到大排序，一个个加入考虑

用一个单调栈维护当前能看到的线，如果当前考虑加入的线和倒数第二条线的交点横坐标小于它与最后一条线的横坐标

那么把最后一条线弹出，重复此过程直到不满足上述条件后把此线加入栈

（这个画个图就能推出来了）

最后还在栈内的就是合法的线了

因为每条线最多被弹出一次所以复杂度 O(n)

注意考虑斜率相同的情况，如果斜率相同只要保留 b 最大的线

最后一定记得把栈内的线按编号从小到大输出

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
    return x*f;
}
const int N=50007;
struct lin
{
    int k,b,id;
    inline bool operator < (const lin &tmp) const {
        return k!=tmp.k ?k<tmp.k : b>tmp.b;
    }
}l[N],st[N];
inline bool cmp(const lin &a,const lin &b){ return a.id<b.id; }
int n;
inline double f(lin a,lin b) { return (double)(a.b-b.b)/(b.k-a.k); }
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        l[i].k=read(); l[i].b=read();
        l[i].id=i;
    }
    sort(l+1,l+n+1);
    int Top=1; st[1]=l[1];
    for(int i=2;i<=n;i++)
    {
        if(l[i].k==st[Top].k) continue;
        while(Top>1 && f(l[i],st[Top])<=f(st[Top],st[Top-1]) )
            Top--;
        st[++Top]=l[i];
    }
    sort(st+1,st+Top+1,cmp);
    for(int i=1;i<=Top;i++) printf("%d ",st[i].id);
    return 0;
}