c3 算法
求某一类在多继承中的继承顺序:
类的mro == [类] + [父类的继承顺序] + [父类2的继承顺序]
如果从左到右的第一个类在后面的顺序中出现,那么就提取出来到mro顺序中
[ABCD] + [EO] --> A = [BCD] + [EO]
如果从左到右的第一个类在后面的顺序中出现,且在后面的顺序中也是第一位,那么就提出来到mro顺序中
[ABCD] + [AEO] --> A = [BCD] + [EO]
如果从左到右的第一个类在后面的顺序中出现,但不是在第一位,那么应该继续往后找,找到符合规则的项目
[ABCD] + [EAO] --> E = [ABCD] + [AO]
[ABCD] + [EAO] + [GEO] --> G = [ABCD] + [EAO] + [EO]
[ABCD] + [EAO] + [EO] --> GE = [ABCD] + [AO] + [O]
关键结论:
这个类没有发生继承,他的顺序永远是[类o]
只要是单继承,不是多继承,那么mro顺序就是从子类到父类的顺序
例子:
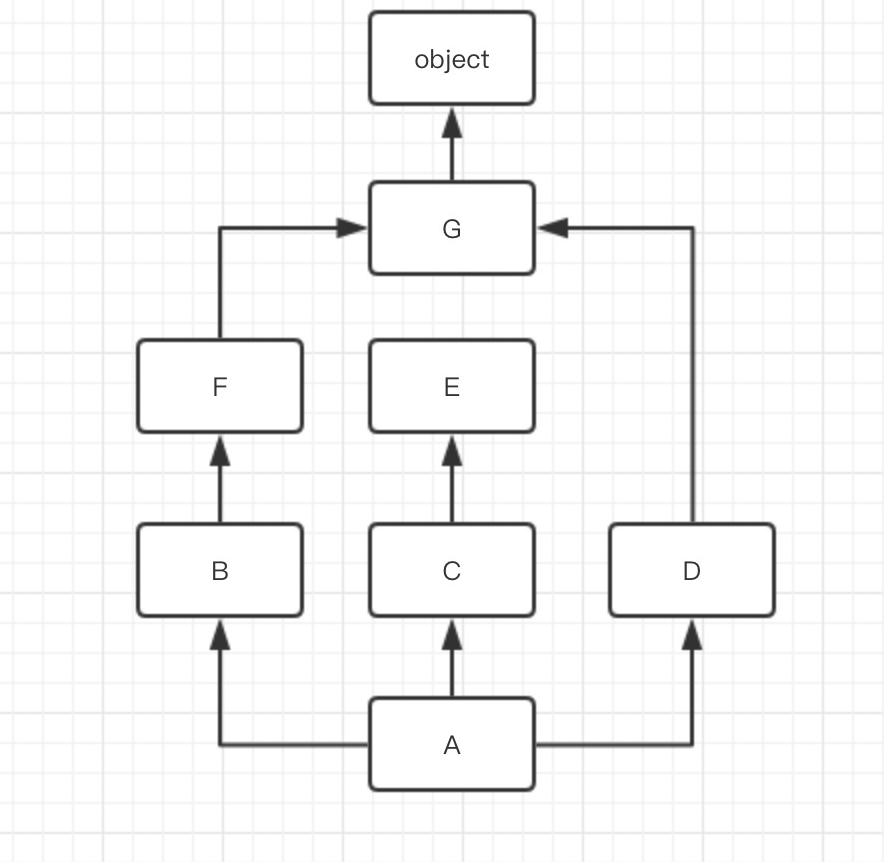
L(G) = [G] + [O]
G = [O]
= GO
L[E] = EO
L[F] = [F] + [GO]
F = [GO]
= FGO
L[B] = [B] + [FGO]
B = [FGO]
BF = [GO]
BFG= [O]
= BFGO
L[C] = [C] + [EO]
C = [EO]
CE = [O]
= CEO
L[D] = [D] + [GO]
D = [GO]
DG = [O]
= DGO
L[A] = [A] + [BFGO] + [CEO] + [DGO]
A = [BFGO] + [CEO] + [DGO]
AB = [FGO] + [CEO] + [DGO]
ABF= [GO] + [CEO] + [DGO]
ABFC= [GO] + [EO] + [DGO]
ABFCE= [GO] + [O] + [DGO]
ABFCED = [GO] + [O] + [GO]
ABFCEDG= [O] + [O] + [O]
= ABFCEDGO
提示:只要是单继承,不是多继承,那么mro顺序就是从子类到父类的顺序
例子2:
L[G] = GO
L[D] = DO
L[E] = EGO
L[F] = FO
L[B] = [B] + [DO] + [EGO]
B = [DO] + [EGO]
BD = [O] + [EGO]
BDE = [O] + [GO]
BDEG = [O] + [O]
= BDEGO
L[C] = [C] + [DO] + [FO]
C = [DO] + [FO]
CD = [O] + [FO]
CDF= [O] + [O]
= CDFO
L[A] = [A] + [BDEGO] + [CDFO]
A = [BDEGO] + [CDFO]
AB = [DEGO] + [CDFO]
ABC = [DEGO] + [DFO]
ABCD = [EGO] + [FO]
ABCDE= [GO] + [FO]
ABCDEG= [O] + [FO]
ABCDEGF= [O] + [O]
L[A] = ABCDEGFO
