T513748 分形树
题目传送门
纪念
思路,对于每一个
比如 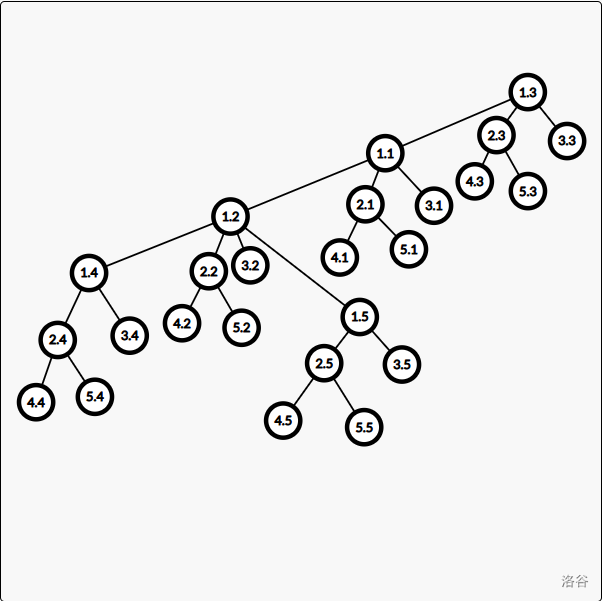
看
const int N = 2e5 + 10;
int n, k, ans1, ans2, max1i, max2i;
struct E{int son;};
vector<E> V[N];
void add(int x, int y) {V[x].push_back({y});}
void dfs(int x, int Fa, int dep)
{
for(auto i:V[x])
{
if(i.son == Fa) continue;
if(ans1 < dep) ans1 = dep, max1i = i.son;
dfs(i.son, x, dep + 1);
}
}
void dfs1(int x, int Fa, int dep)
{
for(auto i:V[x])
{
if(i.son == Fa) continue;
if(ans2 < dep) ans2 = dep, max2i = i.son;
dfs1(i.son, x, dep + 1);
}
}
signed main()
{
read(n); read(k);
rep(i, 2, n)
{
int x, y; read(x); read(y);
add(x, y); add(y, x);
}
dfs(1, 0, 1);
dfs1(max1i, 0, 1);
cout << ans1 * (k - 1) * 2 + ans2 << '\n';
return 0;
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步