A Knight's Journey(dfs)

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 25950		Accepted: 8853

Description

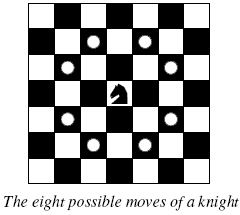Background 
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey 
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans? 

Problem 
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. 
If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

题意：给出p和q,p代表行数（1，2,3....）,q代表列数（A,B,C....）,要求输出骑士从任意一点出发经过所有点的路径，必须按字典序输出；路径不存在输出impossible；

思路：与dfs模板不同的是路径按字典序输出，所以dfs的顺序就不是随意的了，必须按dir[8][2] = {{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}}的顺序；
     而且起点必须是A1,这样得出的路径字典序才最小；

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;

struct node
{
    int row;
    int col;
}way[30];//记录所走路径的行和列

int p,q;
bool vis['Z'+1][27];
int dir[8][2] = {{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}};

bool DFS(struct node* way,int i,int j,int step)
{
    vis[i][j]=true;
    way[step].row=i;
    way[step].col=j;
    if(step==way[0].row)
        return true;

    for(int k=0; k<8; k++)//向八个方向走
    {
        int ii = i+dir[k][0];
        int jj = j+dir[k][1];
        if(!vis[ii][jj] && ii>=1 && ii<=p && jj>=1 && jj<=q)
            if(DFS(way,ii,jj,step+1))
                return true;
    }

    vis[i][j]=false;
    return false;
}

int main()
{
    int test;
    scanf("%d",&test);
    for(int t = 1; t <= test; t++)
    {
        memset(vis,false,sizeof(vis));
        scanf("%d %d",&p,&q);
       
        way[0].row =p*q;

        if(DFS(way,1,1,1))
        {
            cout<<"Scenario #"<<t<<':'<<endl;

            for(int k=1; k<=way[0].row; k++)
                cout<<(char)(way[k].col-1+'A')<<way[k].row;
            cout<<endl<<endl;

        }

        else
        {
            cout<<"Scenario #"<<t<<':'<<endl;
            cout<<"impossible"<<endl<<endl;
        }
    }
    return 0;
}