matlab实现频谱感知-认知无线电

1、前言

\(\quad\) 频谱感知的方法有很多，比如匹配滤波探测，能量检测，静态循环特征探测等方法，然后最近因为在用硬件做能量检测，所以本文主要是说了如何用matlab实现能量检测，它的大概流程就是：信号采样->模平方->累加->判决，其他的方法不再了解。

2、一些前置知识：

（1）数字信号能量、功率计算公式

\(\quad\) 因为数字信号是离散的，所以就直说离散信号能量的计算。

\(\quad\) 设采样后信号为x，长度为N，能量计算为\(energy = \sum\limits_{k = 1}^{N}(x[k])^2\)，放在matlab里计算方法有很多，可以是norm(x)即可。

\(\quad\) 功率计算公式就是，\(power = \cfrac{\sum\limits_{k = 1}^{N}(x[k])^2}{N}\)，放在matlab代码就是norm(x) / N。

\(\quad\) 补充：时域与频域的能量有一个对应关系，\(\sum\nolimits_{n = 1}^{N}|x[n]|^2 = \cfrac{1}{N}\sum\nolimits_{k = 1}^{N}|X[k]|^2\)，其中\(X[k]\)是\(x[n]\)的DFT。

（2）恒虚警率阈值

公式如下：

• 恒虚警率公式

\[P_f = P(D > th|H_0) = Q(\cfrac{\lambda_{P_f} - N\sigma^2_w}{\sqrt{2N\sigma^4_w}}) \]

• 阈值公式

\[\lambda_{P_f} = \sigma^2_w(N + \sqrt{2N}Q^{-1}(P_f)) \]

\(\quad\) 其中\(P_f\)是恒虚警率，\(\lambda_{P_f}\)是阈值，N是信号点数，\(\sigma_w^2\)是噪声的功率，Q是标准正态分布的右尾函数，又叫互补累积分布函数，\(Q(x) = \int_x^{\infty}\cfrac{1}{\sqrt{2\pi}}e^{-\cfrac{t^2}{2}}dt\)，有关这个函数这篇博客正态分布（高斯分布）、Q函数、误差函数、互补误差函数（定义，意义及互相之间的关系）高斯分布的分布概率反解（求门限）会有详细些介绍以及推导，在matlab中计算\(Q^{-1}(x)\)的值可以直接调用erfcinv(x)函数即可。

\(\quad\) 上面是时域的阈值，根据（1）中时域频域的能量对应关系，所以两者的阈值的对应关系就是\(\quad\)\(频域的能量阈值 = 时域的能量阈值 * N\)。

(3) 信号添加噪声

\(\quad\) 在matlab中，加高斯白噪声可以直接使用\(awgn\)函数，比如设原信号为\(x\)，加噪声后的信号为\(y\)，\(SNR = -10\)的信道中，加入噪声可以直接y = awgn(x, SNR, 'measured')，measured参数会自动测量信号的功率，然后通过加噪声将信道信噪比自适应调整到\(SNR\)，具体的用法参考官方，然后加入噪声后可以\(noise = y - x\)提取噪声，从而计算噪声的功率\(P_{noise}\)。

\(\quad\) 上面那种方法简单粗暴，也可以自己加噪声，首先根据信噪比公式\(SNR = 10\lg\cfrac{P_s}{P_{noise}}\)计算出要添加的噪声功率，然后就可以通过公式\(noise = \sqrt{P_{noise}} * randn()\)产生指定功率的噪声信号，matlab里randn()可以产生均值均值为0，方差（功率）\(\sigma^2\)为1，高斯白噪声序列，然后加噪声后的信号就是\(y = x + noise\)，其实两种方法计算出的噪声功率都是差不多大的。

3、频谱感知的matlab实现

\(\quad\) 可以进入正题了，我是计算的频谱的能量，对于每个虚警率\(P_f\)，在\(SNR\)分别等于\(-25，-20，-15，10dB\)的四种信道环境下做100次实验，横轴是虚警率，纵轴是100次实验中检测到的次数，直接给出代码：

clc;
clear all;

N = 1024;%采样点数
n = 1:N;
fs = 1000; %1000hz
t = n / fs; %时间轴

%% original signal
f0 = 100;
f1 = 200;
f2 = 300;
y1 = exp(1i * 2 * pi * f0 * t);
y2 = exp(1i * 2 * pi * f1 * t);
y3 = exp(1i * 2 * pi * f2 * t);
signal = y1 + y2 + y3; 

subplot(5, 2, [1, 2]);
plot(t, signal);
title("signal");
xlabel('t');
ylabel('y');

%% SNR = 10dB
SNR = 10; %信噪比20dB
signal_add_noise = awgn(signal, SNR, 'measured'); %加高斯白噪声
subplot(5, 2, 3);
plot(t, signal_add_noise, 'k');
title("signal + noise (SNR = 10dB)");
xlabel('t');
ylabel('signal + noise');

f = (0 : N-1) * (fs / N);
fft_y = fft(signal_add_noise, N);
abs_fft_y = abs(fft(signal_add_noise, N));

subplot(5, 2, 5);
plot(f, fft_y); %ignore img
title("FFT (SNR = 10dB)");
xlabel("f");
ylabel("y");
grid on;

subplot(5, 2, 7);
plot(f, abs_fft_y); %ignore img
title("abs(FFT) (SNR = 10dB)");
xlabel("f");
ylabel("y");
grid on;

%% SNR = -10dB
SNR = -10; %信噪比20dB
signal_add_noise = awgn(signal, SNR, 'measured'); %加高斯白噪声
subplot(5, 2, 4);
plot(t, signal_add_noise, 'k');
title("signal + noise (SNR = -10db)");
xlabel('t');
ylabel('signal + noise');

f = (0 : N-1) * (fs / N);
fft_y = fft(signal_add_noise, N);
abs_fft_y = abs(fft(signal_add_noise, N));

subplot(5, 2, 6);
plot(f, fft_y); 
title("FFT (SNR = -10dB)");
xlabel("f");
ylabel("y");
grid on;

subplot(5, 2, 8);
plot(f, abs_fft_y); 
title("abs(FFT) (SNR = -10dB)");
xlabel("f");
ylabel("y");
grid on;


%% detect
Pf =(0.01:0.02:1).^2; %虚警概率
%M = 3;
SNR(1) = -25;
SNR(2) = -20;
SNR(3) = -15;
SNR(4) = 10;

for i = 1:length(Pf) %虚警率
    for m = 1 : 4 %信道
        detect_y(i) = 0;
        for kk = 1:100 %次数
            signal_add_noise = awgn(signal, SNR(m), 'measured');
            %signal_energy(i) = sum(abs(signal_add_noise).^2);
            abs_fft_y = abs(fft(signal_add_noise, N));
            signal_add_noise_energy = sum(abs_fft_y.^2);
    
            noise = signal_add_noise - signal; %噪声
            noise_energy = sum(abs(noise).^2); %噪声时域能量
            noise_p(m, kk) = noise_energy / N; %噪声功率
    
            threshold(i) = noise_p(m, kk) * (N + sqrt(2 * N) * sqrt(2) * erfcinv(2 * Pf(i))) * N;
            
            if signal_add_noise_energy > threshold(i)
                detect_y(i) = detect_y(i) + 1;
            end
        end
        detect_diff_channel(m, i) = detect_y(i);
    end
end

subplot(5, 1, 5);
plot(Pf, detect_diff_channel(1, :), '*-b', Pf, detect_diff_channel(2, :), '*-r', ...
    Pf, detect_diff_channel(3, :), '*-g', Pf, detect_diff_channel(4, :), '*-c'); 
legend('SNR = -25dB','SNR = -20dB', 'SNR = -15dB', 'SNR = 10dB');
title("100次实验检测次数");
xlabel("虚警率");
ylabel("检测次数");
grid on;

\(\quad\) 结果：

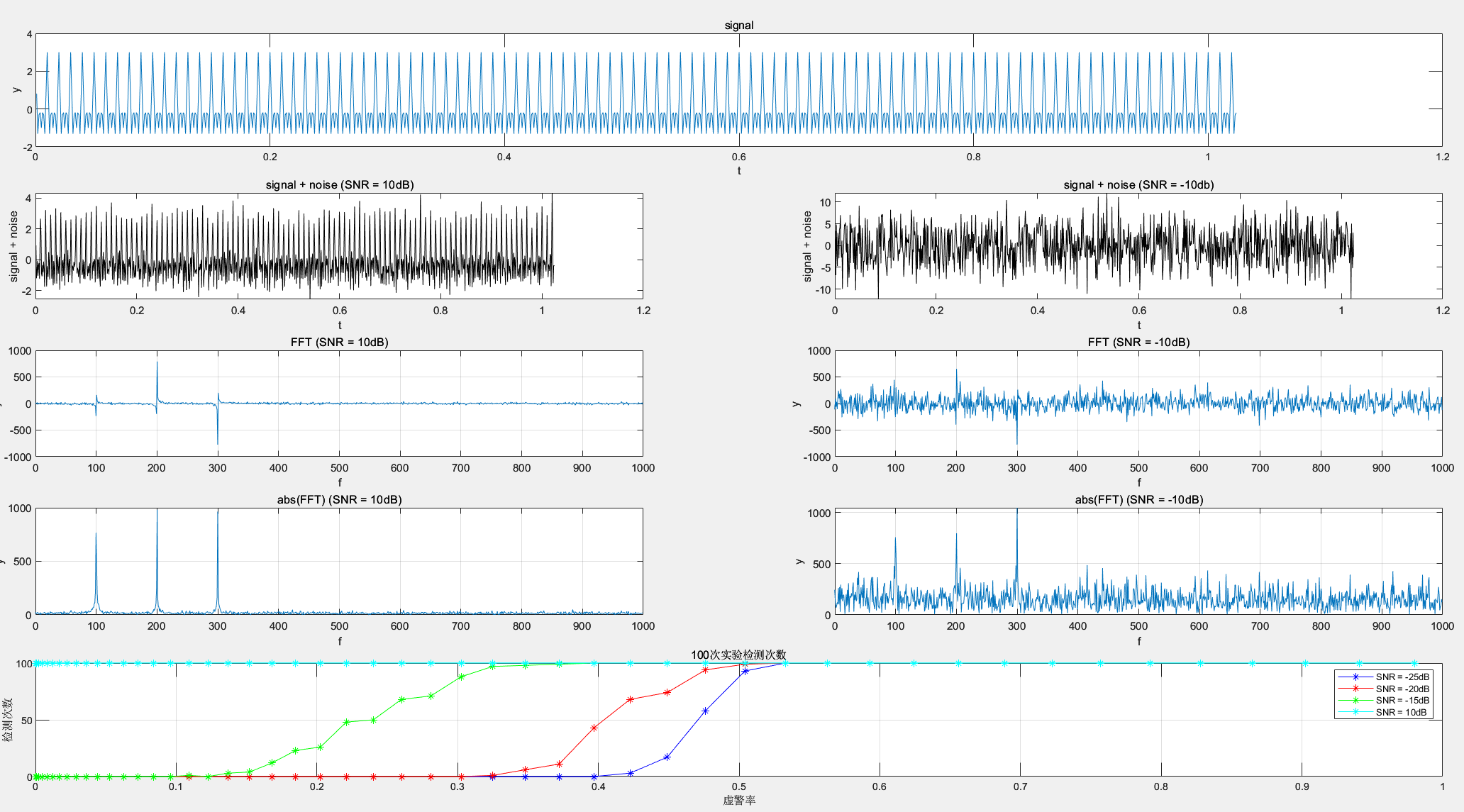
\(\quad\)可以看到相同虚警率下，SNR越大越容易被检测到，当\(SNR > 0\)的时候，检测率基本是\(100\%\)，当\(SNR < 0\)时，原信号失真的厉害，接收方如何解码又是很大的问题。

\(\quad\) 整个过程就差不多这样了，有错误欢迎指正。

参考：
https://blog.csdn.net/Hsaver/article/details/109598769
https://blog.csdn.net/weixin_42647783/article/details/89449048
https://blog.csdn.net/yhcwjh/article/details/113725703
https://blog.csdn.net/Hsaver/article/details/109598769