Educational Codeforces Round 102 (Rated for Div. 2) A~D题

写在前边

链接：Educational Codeforces Round 102 (Rated for Div. 2)

第一场打CF，过了AB两题，不过速度挺慢，C题属实没看懂，D题写了个常规做法之后TLE了还剩下几分钟就睡觉了，想到了用前缀和但是确实不知道该怎么写，最近的目标就先上1400吧。

A. Replacing Elements

链接：A题链接

题目大意:

给定一个数组a, 你可以选任意不同的三个下标$i$, $j$, $k$， 进行操作$a_i=a_j+a_k$，问经过若干次操作之后是否能使得数组中的数$a_i$都小于等于$d$。

思路：

一开始在场上想的是模拟一遍整个过程，最后再检查一下是否合适，看了题解之后根本不用那么麻烦，只需要检查一下数组元素的最大值是否小于等于$d$，或者最小的两个数相加是否小于等于$d$即可，若最大元素小于$d$那么整个数组就符合条件，若最小的两个数相加小于等于$d$，那么他们的和一定可以覆盖所有比$d$大的数，解决。

代码:

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int t, n, d, a[N];

int main() {
    cin >> t;
    while (t--) {
        cin >> n >> d;
        for (int i = 0; i < n; i++) {
            cin >> a[i];
        }
        sort(a, a + n);
        cout << ((a[0] + a[1] <= d || a[n - 1] <= d) ? "YES" : "NO") << endl;
    }

    return 0;
}

B. String LCM

链接：B题链接

题目大意:

找两个字符串的"最小公倍数"即$LCM(s, t)$， 例如$s = "baba"$, $t = "ba"$, 那么$LCM(s, t) = "baba"$，因为$"baba"*1 = "ba" * 2$， $s = "aaa"$, $t = "aa"$, 那么$LCM(s, t) = "aaaaaa"$，因为$"aaa" * 2 = "aa" * 3$。

思路：

先求$GCD(s, t)$，再求$LCM(s, t)$。

1. 求$GCD(s, t)$，它一定是字符串的一个前缀，因此可以枚举所有的前缀，再判断某个前缀变成原来的几倍是否能变成$s,t$，若可以那么就是$GCD(s, t)$。
2. 有了$GCD$再求$LCM$那就是很简单的事了，看代码即可。

代码:

#include <iostream>
#include <string>
#include <algorithm>

using namespace std;

typedef long long ll;

int gcd(int a, int b) {
    while (b != 0) {
        a %= b;
        swap(a, b);
    }
    return a;
}

bool check(string s, string x) {
    string temp = "";
    for (int i = 0; i < s.size(); i++) {
        temp += x;
        if (temp == s) {
            return true;
        }
    }
    return false;
}

string gcd_str(string s, string t) {
    string res = "";
    int lens = s.size(), lent = t.size();
    for (int i = min(lens, lent); i >= 1; i--) {
        if (lens % i == 0 && lent % i == 0) {
            string x = s.substr(0, i);
            if (check(s, x) && check(t, x)) {
                return x;
            }
        }
    }
    return "";
}

int main() {
    int n;
    cin >> n;
    while (n--) {
        string s, t, gcd_st, res = "";
        cin >> s >> t;
        gcd_st = gcd_str(s, t);
        if (gcd_st == "") {
            puts("-1");
            continue;
        }
        int len_gcdst = gcd_st.size();
        int len_lcmst = (s.size() / gcd_st.size()) * (t.size() / gcd_st.size());

        for (int i = 0; i < len_lcmst; i++) {
            res += gcd_st;
        }
        cout << res << endl;
    }

    system("pause");
    return 0;
}

优化：可以用数学的方法求$GCD(s, t)$进行优化，使代码更短，效率更高。

首先判断两个字符串是否存在$GCD(s, t)$可以利用更简单的方法，即 $s + t$ 是否等于 $t + s$，若存在$GCD$，那么$s + t == t + s$，否则就不存在。那证明一下：
如果他们有公因子"abc"，那么$s$就会有$m$个$"abc"$重复，$t$就会有$n$个$"abc"$重复，因此:

$$s + t = m * "abc" + n * "abc" = (m + n) * "abc"$$

而：

$$t + s = n * "abc" + m * "abc" = (n + m) * "abc"$$

得：$(m + n) * "abc" = (n + m) * "abc"$，因此$s + t = t + s$。
那在有解的情况下，最优解的长度就是$gcd(s.size(), t.size())$，如果我们能循环以它的约数为长度的字符串，自然也能循环以它为长度的字符串。
证明不周，详细证明看leetcode 1071. 字符串的最大公因子。
因此优化后的代码：

#include <iostream>
#include <string>
#include <algorithm>

using namespace std;

typedef long long ll;

int gcd(int a, int b) {
    while (b) {
        a %= b;
        swap(a, b);
    }
    return a;
}

string gcd_str(string s, string t) {
    if (s + t != t + s) return "";
    return s.substr(0, gcd(s.size(), t.size()));
}

int main() {
    int n;
    cin >> n;
    while (n--) {
        string s, t, gcd_st, res = "";
        cin >> s >> t;
        gcd_st = gcd_str(s, t);
        if (gcd_st == "") {
            puts("-1");
            continue;
        }
        int len_gcdst = gcd_st.size();
        int len_lcmst = (s.size() / gcd_st.size()) * (t.size() / gcd_st.size());

        for (int i = 0; i < len_lcmst; i++) {
            res += gcd_st;
        }
        cout << res << endl;
    }

    return 0;
}

C. No More Inversions

链接：C题链接

题目大意:

给定一个序列$a$:$1, 2, 3, ..., k-1,k, k-1, k-2, ...k - (n - k)$, 要求构造一个长度为$k$的排列$p$，然后通过$p$构造出$b[i] = p[a[i]]$，要求$b$中的逆序对数量不得多于$a$中逆序对的数量，并且要求$b$的字典序在所有合法方案中最大。

思路：

当时没看懂，今天下午又肝了一下午，看了很多博客才懂了。
首先从$b[i] = p[a[i]]$出发，其实就是$a$数组用来做$p$的下标了，并且若$p$数组中是有序的，那么映射后的$b$数组是跟$a$数组一模一样的。
例如：$a[] = {1, 2, 3, 4, 5, 4, 3}$, $p[] = {1, 2, 3, 4, 5}$, 那么$b[] = {1, 2, 3, 4, 5, 4, 3}$。
若p数组中有两个数调换位置，那么相应的b数组中对应的数也交换，例如$p[] = {1, 2, 3, 5, 4}$，那么b数组中的4和5也相应的发生对换，变成$b[] = {1, 2, 3, 5, 4, 5, 3}$，很神奇。
然后就再找规律发现，我们通过$p$数组改变$b$数组的时候，动的如果是$a$数组对称的那部分，那么逆序对的数量是不会发生变化的，例如上边对称的部分就是${3, 4, 5, 4, 3}$，若改变$p$使得$p$变为$p[] = {1, 2, 4, 3, 5}$, 则对称部分就变成了就变成了${4, 3, 5, 3, 4}$，逆序对的数量仍然没有变化，若改变了前面不对称的部分，那么逆序对就会比$a$多。
最后我们就可以在上边的基础上让$b$的字典序尽量的大，那么就把$p$的大数换到对称部分的最前边即可$p[] = {1, 2, 5, 4, 3}$，此时$b[] = {1, 2, 5, 4, 3, 4, 5}$
至此，solve it!

代码:

#include <iostream>

using namespace std;

int main() {
    int t;
    cin >> t;
    while (t--) {
        int n, k;
        cin >> n >> k;
        int t1 = n - k;
        int t2 = k - t1 - 1;
        for (int i = 1; i <= t2; i++) {
            cout << i << " ";
        }
        for (int i = k; i > t2; i--) {
            cout << i << " ";
        }
        cout << endl;
    }

    return 0;
}

D. Program

链接：D题链接

题目大意:

$x$的初值为$0$，给定一个字符串由$+$,$-$组成，分别使$x$加减$1$，加下来由$m$次操作，每次给定$l，r$,表示将$l-r$（包括$l、r$端点）长度的$+、-$操作屏蔽，求屏蔽后$x$会有多少个不同的值。

思路：

首先明白一点，对于这个题而言，因为一次操作$x$只能变化$1$，因此一个区间内$x$取得的最大值与最小值之差加$1$，那么就是$x$所取得的不同的值，因此我们需要维护一下这个最大值与最小值。
然后访问的时候，删除$l、r$之间的操作后，也就意味着我们不进行这段操作，那我们就需要对上边维护的值进行弥补，那么怎么进行弥补呢，就是$l - r$期间$x$变化的值加到后边，再判断一种很简单的理解方法就是，对于$x$的变化画成一个一个图，中间切开，然后把两边接起来，看下图，中间蓝色切开，再接起来。

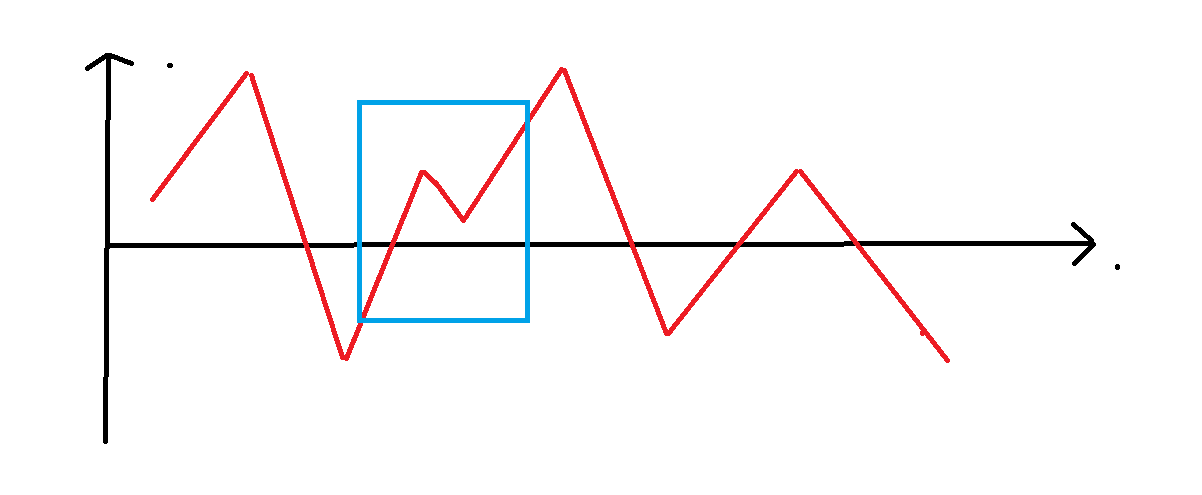
然后就变成了这样。

那什么叫"弥补"呢？就是原来蓝色区间中x的值是上升了，但是若删除蓝色区间操作，那么$x$的就直接把后边的的折线拉下来了，即$x$没有了那段上升操作，即从前一段的重点到后一段的起点，因此，对于前段，不管怎么删除都不受影响，后段会受影响，因此维护最值得时候对于后段给给予"补偿"即可，即后段会减去$x$的变化，因此对于前段，我们从前往后维护，对于后段从后往前维护即可，最后最大值就是前段与后段接起来后的最大值，同理也求得最小值，最后作差 + 1得到$x$的变化。

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 2e5 + 10;
char s[N];
int maxpre[N], minpre[N], maxtail[N], mintail[N];
int a[N], sum[N];

int main() {
    int t;
    cin >> t;
    while (t--) {
        int n, m;
        cin >> n >> m;
        cin >> s + 1;
        for (int i = 1; i <= n; i++) {
            if (s[i] == '+') {
                a[i] = 1;
            } else {
                a[i] = -1;
            }
            sum[i] = sum[i - 1] + a[i];
            maxpre[i] = max(maxpre[i - 1], sum[i]);
            minpre[i] = min(minpre[i - 1], sum[i]);
        }
        maxtail[n + 1] = -1e9, mintail[n + 1] = 1e9;
        for (int i = n; i >= 1; i--) {
            maxtail[i] = max(maxtail[i + 1], sum[i]);
            mintail[i] = min(mintail[i + 1], sum[i]);
        }
        for (int i = 0; i < m; i++) {
            int l, r;
            cin >> l >> r;
            int temp = sum[r] - sum[l - 1];
            int maxN = max(maxpre[l-1], maxtail[r + 1] - temp);
            int minN = min(minpre[l-1], mintail[r + 1] - temp);
            cout << maxN - minN + 1 << endl;
        }
    }
    system("pause");
    return 0;
}