最小生成树（Kruskal Prim）

最小生成树

(克鲁斯卡尔算法) Kruskal

给定一个n个点m条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出impossible。

给定一张边带权的无向图 $G=(V, E)$，其中$V$表示图中点的集合，$E$表示图中边的集合，$n=|V|$，$m=|E|$。

由$V$中的全部$n$个顶点和$E$中$n-1$条边构成的无向连通子图被称为G的一棵生成树，其中边的权值之和最小的生成树被称为无向图G的最小生成树。

输入格式
第一行包含两个整数n和m。

接下来m行，每行包含三个整数$u，v，w$，表示点u和点v之间存在一条权值为w的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出impossible。

数据范围
$1 \leq n \leq 10^5$
$1 \leq m \leq 2∗10^5$
图中涉及边的边权的绝对值均不超过1000。

输入样例：
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例：
6

思路：

$Kruskal$主要用于稀疏图, 用邻接矩阵来处理，时间复杂度为$O(mlogn)$。按照边的权重顺序（从小到大）将边加入生成树中，但是若加入该边会与生成树形成环则不加入该边。直到树中含有$V-1$条边为止。这些边组成的就是该图的最小生成树。

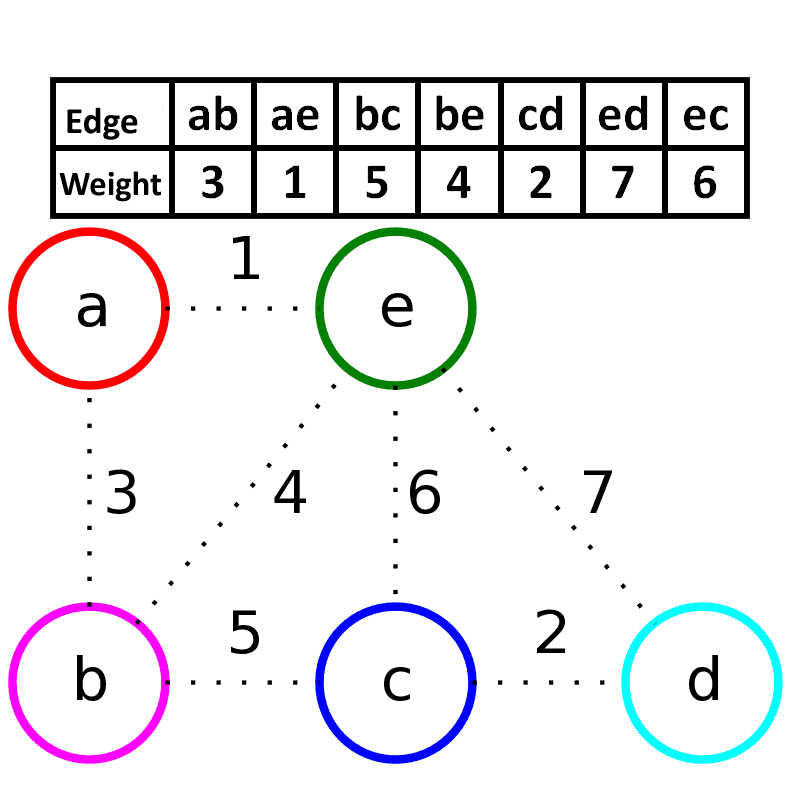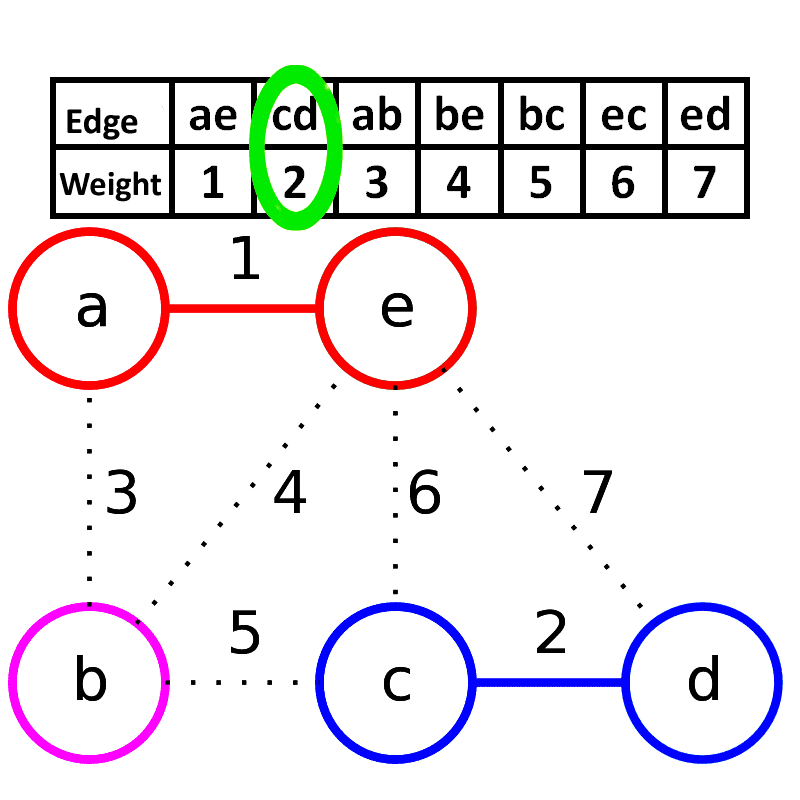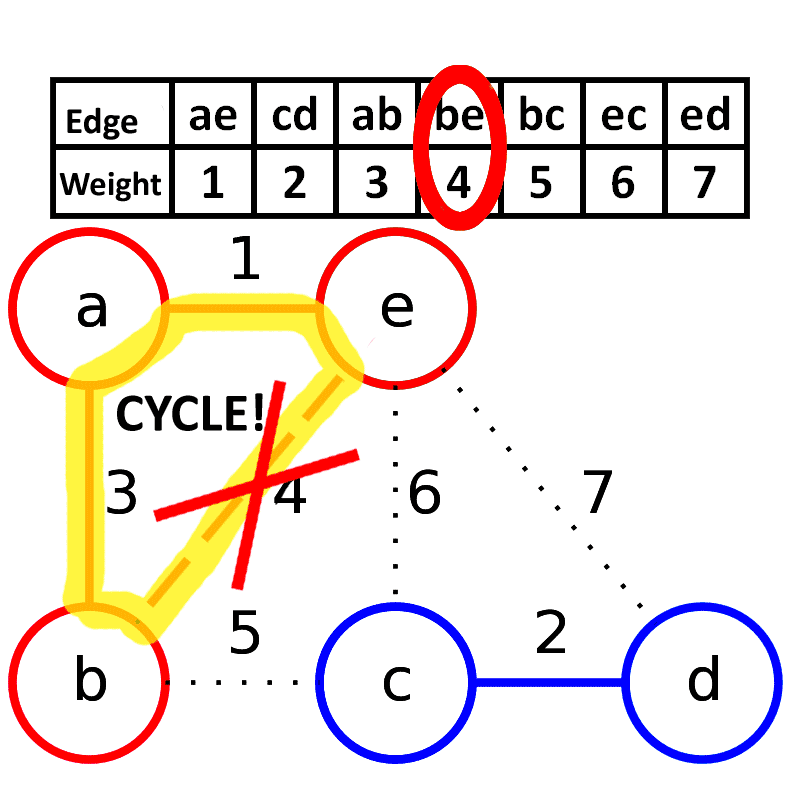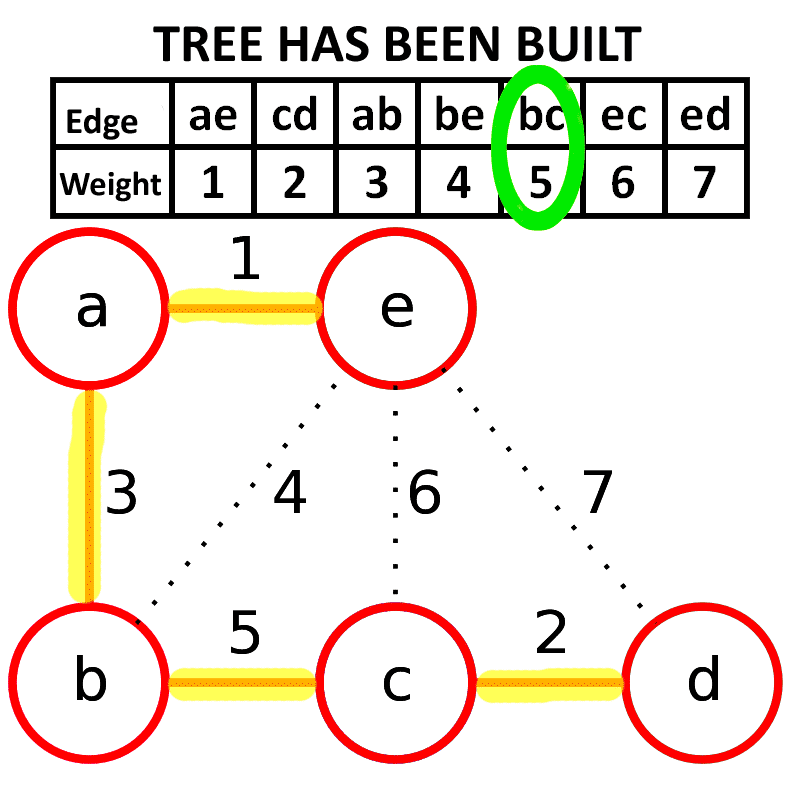
来自维基百科 原作者：Schulllz
其中如果生成树如果与将要加入的边生成环则说明$(a，b)$同祖先, 比如上图那种情况, 因此我们这里就可以使用并查集来判断，如果不会生成环中, 则a != b一定会成立。

代码：

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 100010, M = 200010, INF = 0X3f3f3f3f;

int n, m;
int p[N];

struct Edge
{
    int a, b, w;

    bool operator< (const Edge &W)const //重载运算符
    {
        return w < W.w;
    }
}edges[M];

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m);

    for(int i = 1; i <= n; i++) p[i] = i;

    int res = 0, cnt = 0;
    for(int i = 0; i < m; i++)
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if(a != b)     
        {
            p[a] = b;
            res += w;
            cnt++;
        }
    }

    if(cnt < n-1) return INF; //找不到n-1条边肯定有的不连通
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);

    for(int i = 0; i < m; i++)
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);

        edges[i] = {a, b, w};
    }

    int t = kruskal();

    if(t == INF) puts("impossible");
    else printf("%d\n", t);

    return 0;
}

(普利姆算法) Prim

给定一个n个点m条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出impossible。

给定一张边带权的无向图$G=(V, E)$，其中$V$表示图中点的集合，$E$表示图中边的集合，$n=|V|，m=|E|$。

由$V$中的全部$n$个顶点和$E$中$n-1$条边构成的无向连通子图被称为$G$的一棵生成树，其中边的权值之和最小的生成树被称为无向图$G$的最小生成树。

输入格式
第一行包含两个整数$n$和$m$。

接下来$m$行，每行包含三个整数$u，v，w$表示点$u$和点$v$之间存在一条权值为$w$的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出impossible。

数据范围
$1 \leq n \leq 500$
$1 \leq m \leq 10^5$
图中涉及边的边权的绝对值均不超过10000。

输入样例：
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例：
6

思路

$Prim$主要用于稠密图, 用邻接表来处理，时间复杂度为$O(n^2)$

void Prim()
{
      dist[i] = +∞
      for (int i = 0; i < n; i++)
      {
            1.t<-集合外距离最近的点
            st[t] = true //标记
            2.用t更新其他点到集合的距离
      }
}

代码

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int n, m;
int g[N][N];
int dist[N]; //当前点到集合的距离
bool st[N];

int prim()
{
    memset(dist, 0x3f, sizeof dist);

    int res = 0;
    for(int i = 0; i < n; i++)
    {
        int t = -1;
        for(int j = 1; j <= n; j++) //寻找距离集合最近的点
        {
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
            {
                t = j;
            }
        }

        if(i && dist[t] == INF) return INF; //说明不存在最小生成树  由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树，

        if(i) res += dist[t]; //一定要记得先累加 不然如果存在自环的话更新后再累加会出问题
        st[t] = true;

        for(int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]); //更新
    }

    return res;
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(g, 0x3f, sizeof g);

    while(m--)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);

        g[a][b] = g[b][a] = min(g[a][b], c);
    }

    int t = prim();

    if(t == INF) puts("impossible");
    else printf("%d\n", t);

    return 0;
}