DFS

全排列问题

给定一个整数n，将数字1~n排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式
共一行，包含一个整数n。

输出格式
按字典序输出所有排列方案，每个方案占一行。

数据范围
1≤n≤7
输入样例：
3
输出样例：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

思路：DFS 把所有情况结合起来我们可以将其看作一棵树。
例如题给样例：1 2 3 求其全排列，我们画出这棵树

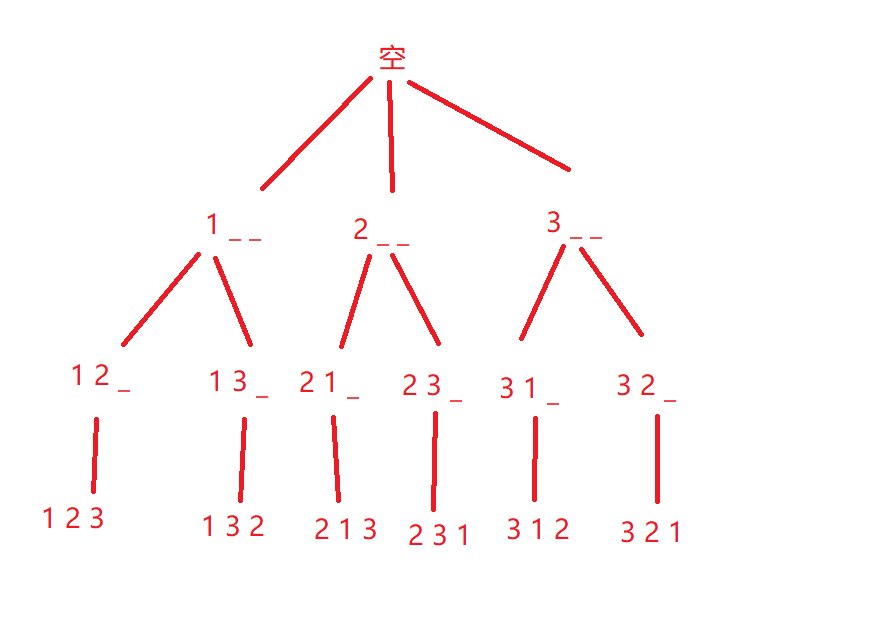
其中我们需要对一些重复的情况则停止搜索，这就是剪枝，例如最左边1 2 _ 之后会有1 2 3或者1 2 1或者1 2 2 几种情况 而后边两种因为我们设置一个状态数组表示已搜，则如果显示已搜则直接停止本次搜索，直到搜索的数字个数到达n个 则输出。

代码：

#include <iostream>

using namespace std;

const int N = 10;
int path[N], n;
bool state[N];

void dfs(int x)
{
    if(x == n)
    {
        for(int i = 0; i < n; i++) printf("%d ", path[i]);
        puts("");
        return;
    }

    for(int i = 1; i <= n; i++)
    {
        if(!state[i])
        {
            path[x] = i;
            state[i] = true;
            dfs(x+1);
            state[i] = false;
        }
    }
}

int main()
{
    cin >> n;

    dfs(0);

    return 0;
}

n皇后问题：

思路：有按行搜与按个搜两种，后者效率有点低，就不说了。
按行搜就是每到一行 枚举行的每一个位置 然后看起列 正斜 反斜 是否已经有皇后 若有则搜索下一个位置 若没有则宣布占领 同时标记其列 正斜 反斜被占领。
直到n个皇后全部放好位置之后就开始输出即可。

其中正斜 假设当前点的坐标为（x，y），则其正斜就是x + y
反斜 假设当前点的坐标为（x，y），则其反斜就是n - x + y 或者 x - y + n，有个n主要是为了防止出现负数的情况

代码：

#include <iostream>

using namespace std;

const int N = 20;
char g[N][N];
bool dg[N], udg[N], col[N]; //dg表示正斜边 udg表示反斜边
int n;

void dfs(int x)
{
    if(x == n)
    {
        for(int i = 0; i < n; i++) puts(g[i]);
        puts("");
        return;
    }

    for(int i = 0; i < n; i++)
    {
        if(!col[i] && !dg[x+i] && !udg[n-x+i])
        {
            col[i] = dg[x+i] = udg[n-x+i] = true;
            g[x][i] = 'Q';
            dfs(x+1);
            g[x][i] = '.';
            col[i] = dg[x+i] = udg[n-x+i] = false;
        }
    }
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
        {
            g[i][j] = '.';
        }
    }

    dfs(0);

    return 0;
}