C++语言实现-拓扑排序

1、拓扑排序的概念

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。

2、拓扑排序的实现步骤

1. 在有向图中选一个没有前驱的顶点并且输出

2. 从图中删除该顶点和所有以它为尾的弧（白话就是：删除所有和它有关的边）

3. 重复上述两步，直至所有顶点输出，或者当前图中不存在无前驱的顶点为止，后者代表我们的有向图是有环的，因此，也可以通过拓扑排序来判断一个图是否有环。

3、拓扑排序过程图示

3.1 如果我们有如下的一个有向无环图，我们需要对这个图的顶点进行拓扑排序，过程如下：

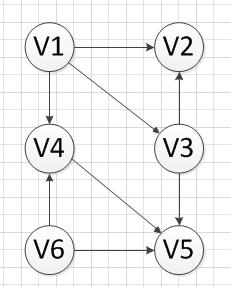
3.2 首先，我们发现V6和v1是没有前驱的，所以我们就随机选去一个输出，我们先输出V6，删除和V6有关的边，得到如下图结果：

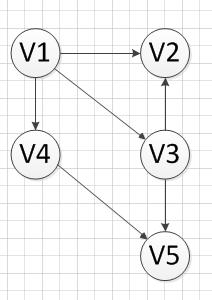
3.3 然后，我们继续寻找没有前驱的顶点，发现V1没有前驱，所以输出V1，删除和V1有关的边，得到下图的结果：

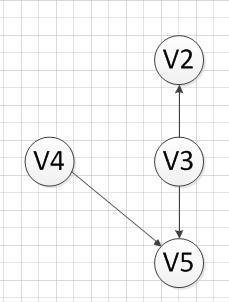
3.4 然后，我们又发现V4和V3都是没有前驱的，那么我们就随机选取一个顶点输出（具体看你实现的算法和图存储结构），我们输出V4，得到如下图结果：

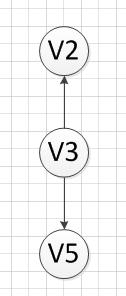
3.5 然后，我们输出没有前驱的顶点V3，得到如下结果：

3.6 然后，我们分别输出V5和V2，最后全部顶点输出完成，该图的一个拓扑序列为：v6–>v1—->v4—>v3—>v5—>v2

4.拓扑排序的代码实现

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int max_v=100;
int main()
{
    int V[max_v];
    int v,e;
    cin>>v>>e;//输入顶点的数目和边的数目
    for(int i=0;i<v;i++)
    {
        V[i]=i+1;//用此数组存放各顶点的值
    }
    int x,y;
    vector<int> G[max_v];
    int in[max_v];//用于存放顶点的入度数
    memset(in,0,sizeof(in));
    for(int i=0;i<e;i++)
    {
        cin>>x>>y;     //输入e对顶点之间的关系
        G[x].push_back(y);///也就是说对于每一个不同的x，G[x].size()会因为所push_back()的y的个数不同而不同
        in[y]++;
    }
    queue<int> que;
    for(int i=0;i<v;i++)
    {
        if(in[V[i]]==0)//如果顶点i的入度为零，入栈
            que.push(V[i]);
    }
   int flag=1;
   while(!que.empty())
   {
       if(flag==1)
            flag=0;
       else
            cout<<',';
        int top=que.front();
        que.pop();
        cout<<top;
       for(int i=0;i<G[top].size();i++)///此处参考上方所说的G[x].size()的得来，所以G[top].size()所表示的就是与top顶点相连的顶点数目,
　　　　{　　　　　　　　　　　　　　　　　　 　//要执行G[top].size()次循环，将与top相连的所有顶点的入度数减1in[G[top][i]]--;
           if(in[G[top][i]]==0)
                que.push(G[top][i]);
       }
   }
    return 0;
}

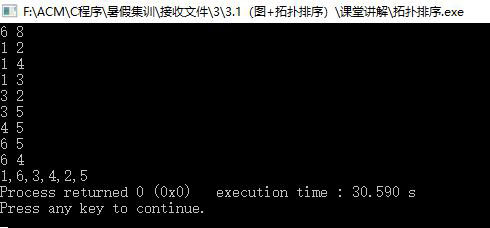
输入：

输出：

进击的巨人

C++语言实现-拓扑排序

2、拓扑排序的实现步骤

公告