Aladdin and the Flying Carpet（唯一分解定理）

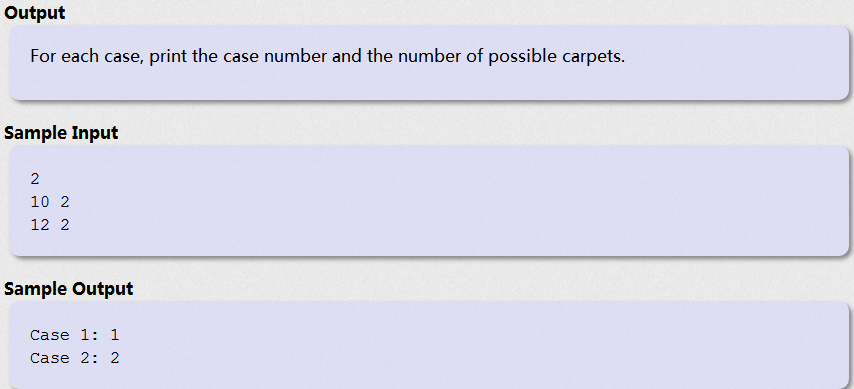
题目大意：给两个数a，b，求满足c*d==a且c>=b且d>=b的c,d二元组对数，(c,d)和(d,c)属于同一种情况；

题目分析：根据唯一分解定理，先将a唯一分解，则a的所有正约数的个数为num = (1 + a1) * (1 + a2) *...(1 + ai)，这里的ai是素因子的指数，见唯一分解定理，因为题目说了不会存在c==d的情况，因此num要除2，去掉重复情况，然后枚举小于b的a的约数，拿num减掉就可以了。

首先了解唯一分解定理：

 

题目思路：根据唯一分解定理有:

1.每个数n都能被分解为：n=p1^a1*p2^a2*^p3^a3……pn^an(p为素数);

2.n的正因数的个数sum为：sum=（1+a1）*(1+a2)*(1+a3)……(1+an);

最短边为m，若m>=sqrt（n），则无解。所以m最多我10^6，可遍历找出1-m中n的因子，并用sum去减去这类因子的个数。

代码解析：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define ll long long
using namespace std;
int const MAX = 1e6 + 10;
int p[MAX];//用于存素数
bool u[MAX];//u[i]标记数字i是否为素数
int num, cnt;
ll a, b, tmp;
 
void get_prime()  
{  
    memset(u, false, sizeof(u));
    for(int i = 2; i <= sqrt(MAX); i++)
        if(!u[i])
            for(int j = i * i; j <= MAX; j += i)
                u[j] = true;
    for(int i = 2; i <= MAX; i++)
        if(!u[i])
            p[cnt ++] = i;
}

//唯一分解定理的正体
void cal()
{
    for(int i = 0; i < cnt && p[i] <= sqrt(tmp); i++)
    {
        int cc = 0;
        while(tmp % p[i] == 0)
        {
            cc ++;
            tmp /= p[i];
        }
        num *= (cc + 1);
 
    }
    if(tmp > 1) //如果tmp不能被整分，说明还有一个素数是它的约数，此时cc=1
        num *= 2;
}
 
int main()
{
    int T;
    scanf("%d", &T);
    cnt = 0;
    get_prime();
    for(int ca = 1; ca <= T; ca++)
    {
        scanf("%lld %lld", &a, &b);
        if(a < b * b)
            printf("Case %d: 0\n", ca);
        else
        {
            num = 1;
            tmp = a;
            cal();
            num /= 2;
            for(int i = 1; i < b; i++)
                if(a % i == 0)
                    num --;
            printf("Case %d: %d\n", ca, num);
        }
    }
}

 扩展：对一个数N进行分解，求出其分解的结果；

void add_integer(int n,int d)
{
    for(int i=0; i<len; i++)
    {
        while(n % primes[i] == 0)
        {
            n /= primes[i];
            e[i] += d;
        }
        if(n == 1)//提前结束，节约时间
            break;
    }
}

n是我们要分解的数字，当n在分子上的时候d为1，在分母上的时候d为-1；e数组表示的是i这个数能够分解成几个primes[i]相乘存的数值是primes[i]的次方。

最后把这些数在相乘就可以了。

例如：

100经过分解之后得到的是

e[i]:           2 0 2

primes[i]:  2 3 5

相乘得2^2*5^2=100。