Working out（DP）
题目描述：
题意：
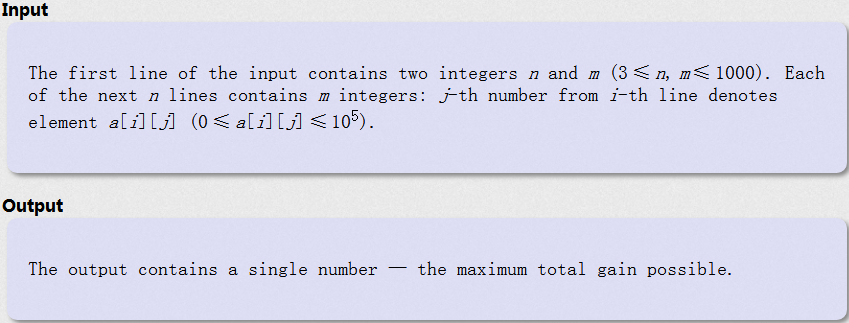
有n*m个格子, 走过一个格子可以得到相应的分数.
A 从(1,1)沿 下 或 右 走到(n,m)
B 从(n,1)沿 上 或 右 走到(1,m)
两人路径有且只能有一个格子重合(重合格子的分数不算), 求两人分数之和的最大值.
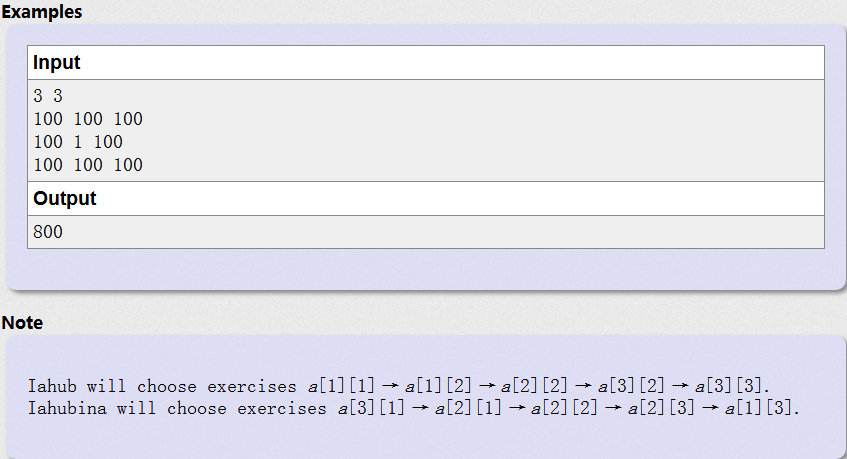
首先要保证只有一个格子重合,那么只可能是以下两种情况:
1) A向右走,相遇后继续向右走,而B向上走,相遇后继续向上走
2) A向下走,相遇后继续向下走,而B向右走,相遇后继续向右走
接着枚举相遇的格子(i,j)即可,考虑四个方向的dp
dp1[i][j] := 从 (1, 1) 到 (i, j) 的最大分数
dp2[i][j] := 从 (i, j) 到 (n, m) 的最大分数
dp3[i][j] := 从 (n, 1) 到 (i, j) 的最大分数
dp4[i][j] := 从 (i, j) 到 (1, m) 的最大分数
代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 const int maxn=1e3+5; 6 int a[maxn][maxn]; 7 int dp1[maxn][maxn];//(1,1)-(i,j) 8 int dp2[maxn][maxn];//(i,j)-(1,1) 9 int dp3[maxn][maxn];//(n,1)-(i,j) 10 int dp4[maxn][maxn];//(i,j)-(n,1) 11 int main() 12 { 13 int n,m; 14 scanf("%d%d",&n,&m); 15 for(int i=1;i<=n;i++) 16 for(int j=1;j<=m;j++) scanf("%d",&a[i][j]); 17 for(int i=1;i<=n;i++) 18 for(int j=1;j<=m;j++) dp1[i][j]=a[i][j]+max(dp1[i][j-1],dp1[i-1][j]); 19 for(int i=n;i>=1;i--) 20 for(int j=m;j>=1;j--) 21 dp2[i][j]=a[i][j]+max(dp2[i][j+1],dp2[i+1][j]); 22 for(int i=n;i>=1;i--) 23 for(int j=1;j<=m;j++) 24 dp3[i][j]=a[i][j]+max(dp3[i+1][j],dp3[i][j-1]); 25 for(int i=1;i<=n;i++) 26 for(int j=m;j>=1;j--) 27 dp4[i][j]=a[i][j]+max(dp4[i][j+1],dp4[i-1][j]); 28 int ans=0; 29 for(int i=2;i<n;i++) 30 for(int j=2;j<m;j++) 31 { 32 ans=max(ans,dp1[i][j-1]+dp2[i][j+1]+dp3[i+1][j]+dp4[i-1][j]); 33 ans=max(ans,dp3[i][j-1]+dp4[i][j+1]+dp2[i+1][j]+dp1[i-1][j]); 34 } 35 printf("%d\n",ans); 36 return 0; 37 }
样例中的dp1,dp2,dp3,dp4最终结果为：
100 200 300 200 201 400 300 400 500 500 400 300 400 201 200 300 200 100 300 400 500 200 201 400 100 200 300 300 200 100 400 201 200 500 400 300
在最终求出结果时：
for(int i=2;i<n;i++)
{
for(int j=2;j<m;j++)
{
ans=max(ans,dp1[i][j-1]+dp2[i][j+1]+dp3[i+1][j]+dp4[i-1][j]);
ans=max(ans,dp3[i][j-1]+dp4[i][j+1]+dp2[i+1][j]+dp1[i-1][j]);
}
}
第一种情况下的ans的值为黄色部分值相加，第二种情况下的ans的值为蓝色部分值相加；
