Number String（DP）

题目：

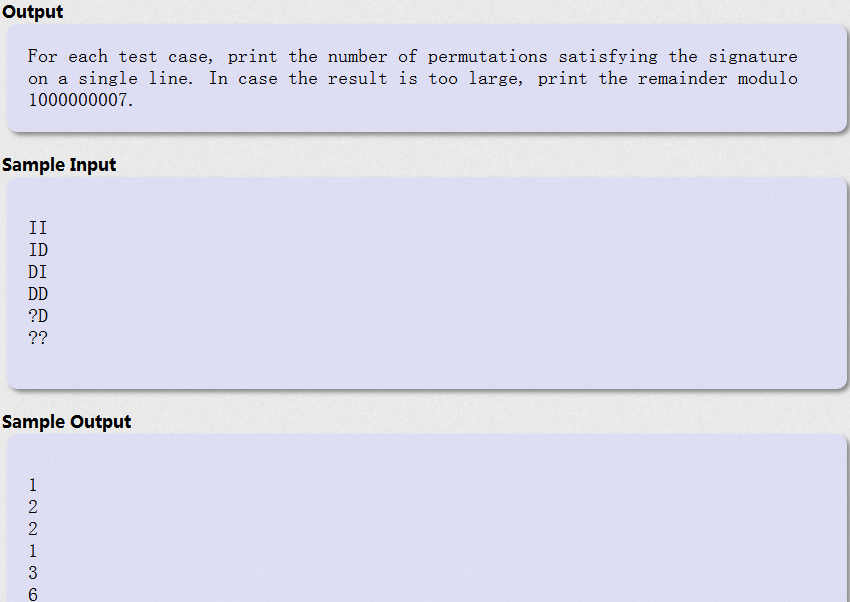
题意：

　　给你一个字符串s，s[i] = 'D'表示排列中a[i] > a[i+1]，s[i] = 'I'表示排列中a[i] < a[i+1]。

　　比如排列 {3, 1, 2, 7, 4, 6, 5} 表示为字符串 DIIDID。

解题思路：

　　　用一个二维数组dp[i][j]表示：长度为 i ，以数字 j 结尾的数字串的排列有多少种，dp[0][1]=1是确定了的。

    但是在状态转移的时候，我们不得不考虑前面选了什么，也就是状态的设定是有后效性的，
    所以考虑给状态再添一层含义：必须选前i个元素。
    那么这样岂不是每次只能选i吗？那么第二维岂不是没有用了？
    所以我们考虑用j把i替换出来，那么在状态转移的时候就需要考虑放入i时，怎么替换能使原来的大小顺序保持不变。
    将dp[i-1][j]的i-1个数的序列中 ≥j 的数都加1，这样i-1变成了i，j变成了j+1，而j自然就补在后面了。
    处理I：dp[i][j] = Σdp[i-1][x]，其中1≤x≤j-1，可进一步简化，dp[i][j] = dp[i][j-1]+dp[i-1][j-1]
    处理D：dp[i][j] = Σdp[i-1][x]，其中j≤x≤i-1，可进一步简化，dp[i][j] = dp[i-1][j+1]+dp[i-1][j]
    处理?：dp[i][j] = Σdp[i-1][x]，其中1≤x≤i-1 

代码：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
const LL mod=1e9+7;
const int N=1005;
char s[N];
LL dp[N][N];

int main()
{
    while(scanf("%s",s+1)!=EOF)
    {
        int len=strlen(s+1);
        memset(dp,0,sizeof(dp));
        dp[0][1]=1;
        for(int i=1;i<=len;i++)
        {
            if(s[i]=='I')
                for(int j=2;j<=i+1;j++)
                    dp[i][j]=(dp[i][j-1]+dp[i-1][j-1])%mod;
            else if(s[i]=='D')
                for(int j=i;j>=1;j--)
                    dp[i][j]=(dp[i][j+1]+dp[i-1][j])%mod;
            else
            {
                for(int j=1;j<=i+1;j++)
                    dp[i][j]=(dp[i][j-1]+dp[i-1][j-1])%mod;
                LL sum=0;
                for(int j=i;j>=1;j--)
                {
                    sum=(sum+dp[i-1][j])%mod;
                    dp[i][j]=(dp[i][j]+sum)%mod;
                }
            }
        }
        LL ans=0;
        for(int i=1;i<=len+1;i++) ans=(ans+dp[len][i])%mod;
        printf("%lld\n",ans);
    }
    return 0;
}