最小生成树
转载自:https://blog.csdn.net/yeruby/article/details/38615045
MST(Minimum Spanning Tree,最小生成树)问题有两种通用的解法,Prim算法就是其中之一,它是从点的方面考虑构建一颗MST,大致思想是:设图G顶点集合为U,首先任意选择图G中的一点作为起始点a,将该点加入集合V,再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小,此时将b点也加入集合V;以此类推,现在的集合V={a,b},再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小,此时将c点加入集合V,直至所有顶点全部被加入V,此时就构建出了一颗MST。因为有N个顶点,所以该MST就有N-1条边,每一次向集合V中加入一个点,就意味着找到一条MST的边。
用图示和代码说明:
初始状态:
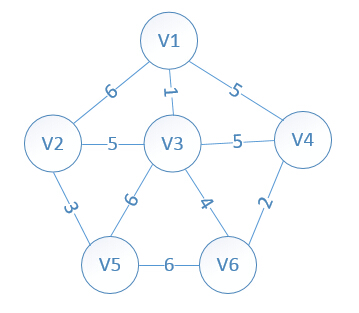
设置2个数据结构:
lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST
mst[i]:表示对应lowcost[i]的起点,即说明边<mst[i],i>是MST的一条边,当mst[i]=0表示起点i加入MST
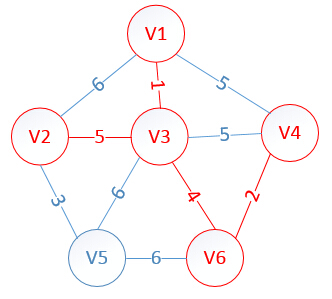
我们假设V1是起始点,进行初始化(*代表无限大,即无通路):
lowcost[2]=6,lowcost[3]=1,lowcost[4]=5,lowcost[5]=Maxcost,lowcost[6]=Maxcost
mst[2]=1,mst[3]=1,mst[4]=1,mst[5]=1,mst[6]=1,(所有点默认起点是V1)
明显看出,以V3为终点的边的权值最小=1,所以边<mst[3],3>=1加入MST,<mst[3],3>表示以mst[3]为起点,3为终点的边
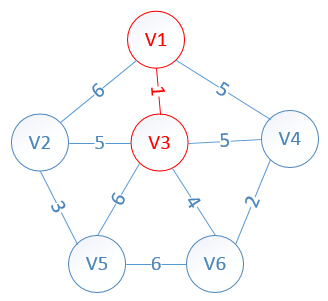
此时,因为点V3的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=5,lowcost[5]=6,lowcost[6]=4
mst[2]=3,mst[3]=0,mst[4]=1,mst[5]=3,mst[6]=3(可以理解为: 2 的起点为 3 , 4 的起点为 1 , 5 的起点为 3 , 6 的起点为 3 )
明显看出,以V6为终点的边的权值最小=4,所以边<mst[6],6>=4加入MST
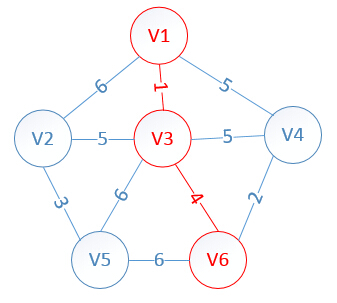
此时,因为点V6的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=2,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=6,mst[5]=3,mst[6]=0
明显看出,以V4为终点的边的权值最小=2,所以边<mst[4],4>=4加入MST
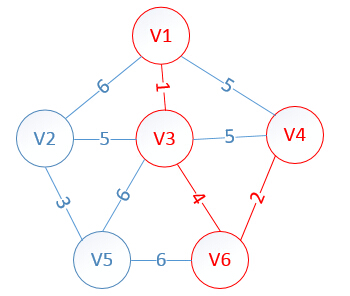
此时,因为点V4的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=0,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=0,mst[5]=3,mst[6]=0
明显看出,以V2为终点的边的权值最小=5,所以边<mst[2],2>=5加入MST
此时,因为点V2的加入,需要更新lowcost数组和mst数组:
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=3,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=2,mst[6]=0
很明显,以V5为终点的边的权值最小=3,所以边<mst[5],5>=3加入MST
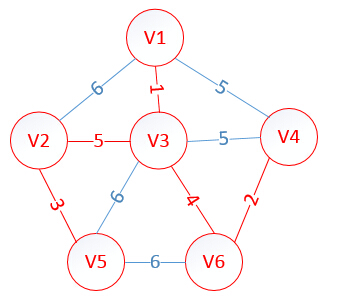
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=0,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=0,mst[6]=0
至此,MST构建成功,如图所示:
根据上面的过程,可以容易的写出具体实现代码如下(cpp):
代码实现:
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 #define MAX 100 5 #define MAXCOST 0x7fffffff 6 7 int graph[MAX][MAX]; 8 9 int prim(int graph[][MAX], int n) 10 { 11 int lowcost[MAX];//lowcost[i]:表示以i为终点的边的最小权值,注意i的起点并不确定 12 int mst[MAX];//mst[i]:表示对应lowcost[i]的起点 13 int i, j, min, minid, sum = 0; 14 //我们设V1是起点,进行初始化 15 for (i = 2; i <= n; i++) 16 { 17 lowcost[i] = graph[1][i];//如果该顶点未与V1相连,lowcost值为MAXCOST 18 mst[i] = 1;//刚开始的时候,对于每一个Vi来说,它的起点都是V1 19 } 20 mst[1] = 0;//当mst[i]=0表示起点i加入MST 21 for (i = 2; i <= n; i++)//执行n-1次,保证V1到达每个顶点的最短边都能够找到 22 { 23 min = MAXCOST; 24 minid = 0;//起点V1到顶点minid的边最短 25 for (j = 2; j <= n; j++)//找出最短的边,用minid记录下该顶点,用min存下最短边 26 { 27 if (lowcost[j] < min && lowcost[j] != 0) 28 { 29 min = lowcost[j]; 30 minid = j; 31 } 32 } 33 cout << "V" << mst[minid] << "-V" << minid << "=" << min << endl; 34 sum += min;//每找出一条最短边就加到权值中去 35 lowcost[minid] = 0;//当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST 36 for (j = 2; j <= n; j++) 37 { 38 if (graph[minid][j] < lowcost[j]) 39 { 40 lowcost[j] = graph[minid][j]; 41 mst[j] = minid; 42 } 43 } 44 } 45 return sum; 46 } 47 48 int main() 49 { 50 int i, j, k, m, n; 51 int x, y, cost; 52 //ifstream in("input.txt"); 53 cin >> m >> n;//m=顶点的个数,n=边的个数 54 //初始化图G 55 for (i = 1; i <= m; i++) 56 { 57 for (j = 1; j <= m; j++) 58 { 59 graph[i][j] = MAXCOST; 60 } 61 } 62 //构建图G 63 for (k = 1; k <= n; k++) 64 { 65 cin >> i >> j >> cost; 66 graph[i][j] = cost; 67 graph[j][i] = cost; 68 } 69 //求解最小生成树 70 cost = prim(graph, m); 71 //输出最小权值和 72 cout << "Minimum weight sum=" << cost << endl; 73 return 0; 74 }
Input:
6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6
Output:
V1-V3=1
V3-V6=4
V6-V4=2
V3-V2=5
V2-V5=3
最小权值和=15



 浙公网安备 33010602011771号
浙公网安备 33010602011771号