线段树-hdu3397
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3397
题目描述:
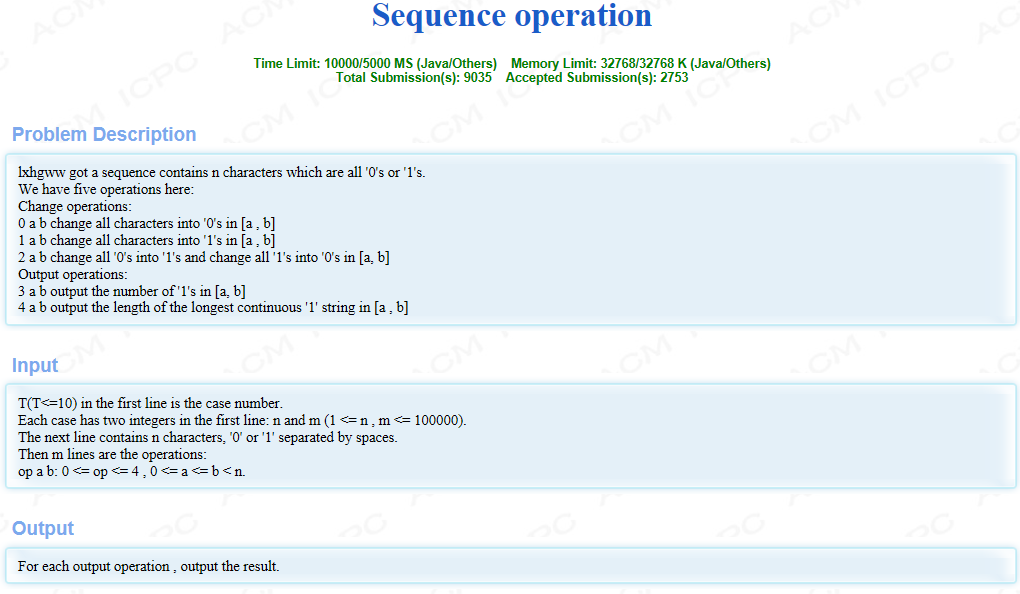
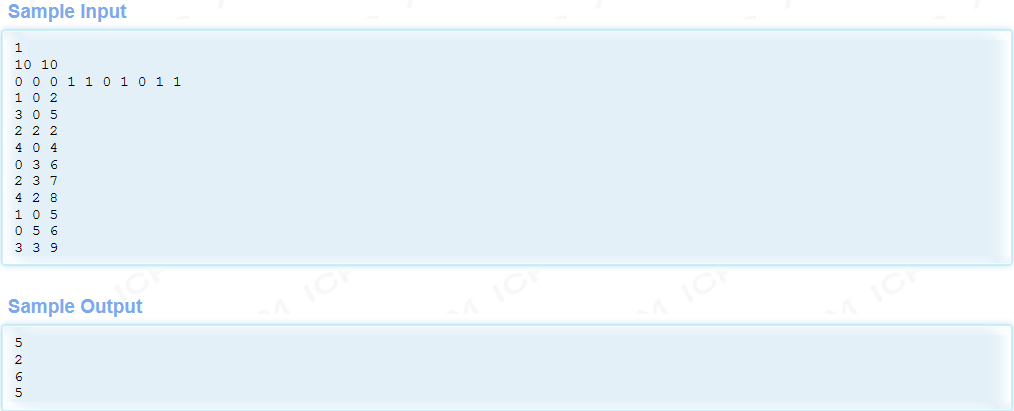
题目大意:给我们一串二进制串,需要我们对其进行以下操作:
1、输入0,a,b,将a,b范围内的所有二进制数字变为0;
2、输入1,a,b,将a,b范围内的所有二进制数字变为1;
3、输入2,a,b,将a,b范围内的所有二进制数字0变为1,1变为0;
4、输入3,a,b,统计a,b范围内的二进制数字1的个数并输出;
4、输入4,a,b,统计a,b范围内的最长连续的1个数并输出;
代码实现:
#include <cstdio> #include <algorithm> using namespace std; const int MAXN =1e6; int N,M; struct node{ /**val记录 0,1操作——赋值 初始值为-1; val=0表示将当前节点(x)范围内的值全部赋值为0 val=1表示将当前节点(x)范围内的值全部赋值为1 flag记录2操作 ——转换 默认值为0; flag=1表示将当前节点(x)范围内的0全部转换为1,1全部转换为0 lmax_0记录x范围内从左开始连续的0的长度 rmax_0记录x范围内从右开始连续的0的长度 max_0记录x范围内最长连续的0的长度 sum_0记录x范围内0的个数 同理,lmax_1,rmax_1,max_1,sum_1是用来记录1的*/ int l,r,val,flag; int lmax_0,rmax_0,max_0,sum_0; int lmax_1,rmax_1,max_1,sum_1; int len(){return r-l+1;}//记录每个节点区间的总长度 int mid(){return (r+l)/2;} void change(int a,int rev){ if(a==0){//0操作 lmax_0=rmax_0=max_0=sum_0=len(); lmax_1=rmax_1=max_1=sum_1=0; val=a;flag=0; }else if(a==1){//1操作 lmax_0=rmax_0=max_0=sum_0=0; lmax_1=rmax_1=max_1=sum_1=len(); val=a;flag=0; } if(rev){//如果rev=1,执行2操作 swap(lmax_0,lmax_1);swap(rmax_0,rmax_1); swap(max_0,max_1);swap(sum_0,sum_1); flag^=1;//即flag由0变为1 } } }tree[MAXN*4]; int a[MAXN]; ///push_up(tree[1],tree[2],tree[3]); void push_up(node &a,node &b,node &c){ //更新x节点的lmax_0、rmax_0、max_0、sum_0 //以及x节点的lmax_1、rmax_1、max_1、sum_1 a.lmax_0=b.lmax_0;a.rmax_0=c.rmax_0;//父亲的左边最长0串=左子树的左边最长0串,父亲的右边最长0串=右子树的右边最长0串 a.lmax_1=b.lmax_1;a.rmax_1=c.rmax_1; a.sum_0=b.sum_0+c.sum_0; a.sum_1=b.sum_1+c.sum_1;//父亲总的0的个数=左子树0的个数+右子树0的个数,父亲总的1的个数=左子树1的个数+右子树1的个数 a.max_0=max(max(b.max_0,c.max_0),(b.rmax_0+c.lmax_0));///如果出现像0000001011这种情况,a.max_0的值就应该为b.rmax_0+c.lmax_0 a.max_1=max(max(b.max_1,c.max_1),(b.rmax_1+c.lmax_1)); if(b.len()==b.lmax_0) a.lmax_0+=c.lmax_0;///比如像0000011011这种情况,注意a.lmax_0在刚开始就已经赋值为b.lmax_0了,这只是再次判断以防万一 if(b.len()==b.lmax_1) a.lmax_1+=c.lmax_1; if(c.len()==c.rmax_0) a.rmax_0+=b.rmax_0; if(c.len()==c.rmax_1) a.rmax_1+=b.rmax_1; } ///build(1,0,N-1);//第一个节点的区间的左右的值分别为0,N-1 void build(int x,int l,int r){ tree[x].l=l;tree[x].r=r; tree[x].lmax_0=tree[x].rmax_0=0; tree[x].lmax_1=tree[x].rmax_1=0; tree[x].max_0=tree[x].max_1=0; tree[x].sum_0=tree[x].sum_1=0; tree[x].flag=0;tree[x].val=-1; if(l==r){ tree[x].change(a[l],0); return ; } int mid=(l+r)/2; build(x<<1,l,mid); build(x<<1|1,mid+1,r); push_up(tree[x],tree[x<<1],tree[x<<1|1]); } ///if(a==0||a==1||a==2) update(1,b,c,a); /* 0用于将范围内所有的数变为0,1用于将范围内所有的数变为1,2用于将范围内所有的0变为1,1变为0 */ void update(int x,int l,int r,int val){ int L=tree[x].l,R=tree[x].r; if(l<=L && R<=r){///[L,R]包含于[l,r] if(val==0||val==1) tree[x].change(val,0);//这一步即能实现将值进行转换 else tree[x].change(-1,1);//这一步实现2操作 return ; } //push_down的作用,实现向下更新 if(tree[x].val!=-1||tree[x].flag)//仅针对于刚刚更新的节点来说,即上方代码实现将当前节点与该节点以上的节点更新后, //接下来的节点tree[x].val已经改变了,所以需要对其左右子区间进行更新 { tree[x<<1].change(tree[x].val,tree[x].flag); tree[x<<1|1].change(tree[x].val,tree[x].flag); tree[x].val=-1;tree[x].flag=0; } int mid=(L+R)/2; ///如果mid直接处在l的右边就只更新左区间(条件1),处在r的左边就只更新右区间(条件2),如mid处在[l,r]之间,需要更新左右区间(条件1+2) if(mid>=l) update(x<<1,l,r,val); if(mid<r) update(x<<1|1,l,r,val); push_up(tree[x],tree[x<<1],tree[x<<1|1]); } int query(int x,int l,int r,int val) { int L=tree[x].l,R=tree[x].r; if(l<=L && R<=r) { if(val==3) return tree[x].sum_1; else return tree[x].max_1; } int mid=(L+R)/2; //push_down的作用,实现向下更新 if(tree[x].val!=-1||tree[x].flag) { tree[x<<1].change(tree[x].val,tree[x].flag); tree[x<<1|1].change(tree[x].val,tree[x].flag); tree[x].val=-1;tree[x].flag=0; } if(r<=mid) return query(x<<1,l,r,val); else if(l>mid) return query(x<<1|1,l,r,val); else { int max1=query(x<<1,l,r,val); int max2=query(x<<1|1,l,r,val); if(val==3) return max1+max2; int max3=min(tree[x<<1].r-l+1,tree[x<<1].rmax_1)+min(r-tree[x<<1|1].l+1,tree[x<<1|1].lmax_1); return max(max(max1,max2),max3); } } int main(){ int T;scanf("%d",&T); while(T--){ scanf("%d%d",&N,&M); for(int i=0;i<N;i++) scanf("%d",&a[i]); build(1,0,N-1); while(M--){ int a,b,c; scanf("%d%d%d",&a,&b,&c); if(a==0||a==1||a==2) update(1,b,c,a); else printf("%d\n",query(1,b,c,a));//如果a等于3,输出[b,c]之间1的个数,a=4输出[b,c]之间最长连续1的个数 } } return 0; }4




 浙公网安备 33010602011771号
浙公网安备 33010602011771号