NOIP模拟测试on 2019.9.27
T1 string

面对1e5的数据范围,暴力sort肯定不行,而我一开始连sort都能写错,真是傻逼到了极点。
考虑用线段树维护,我们看题目中只有26个小写字母,就可以维护每个区间对应的字母,修改时就做26次区间赋值操作。

#include<bits/stdc++.h> using namespace std; const int maxn=1e6+7; struct node{ int l,r,v; }tree[maxn*4]; char str[maxn]; int n,m,l,r,opt; int f[maxn];//一个区间中'a'-'z'字母的个数 void ljb(){ freopen("string.in","r",stdin); freopen("string.out","w",stdout); } void build(int now,int l,int r){ tree[now].l=l,tree[now].r=r; if(l==r){ tree[now].v=str[l]-'a'+1; return; } int mid=(l+r)>>1; build(now<<1,l,mid); build(now<<1|1,mid+1,r); if(tree[now<<1].v==tree[now<<1|1].v) tree[now].v=tree[now<<1].v; } void update(int now,int l,int r){ if(tree[now].l>=l&&tree[now].r<=r&&tree[now].v){ f[tree[now].v]+=tree[now].r-tree[now].l+1; return; } if(tree[now].v) tree[now<<1].v=tree[now<<1|1].v=tree[now].v; int mid=(tree[now].l+tree[now].r)>>1; if(l<=mid) update(now<<1,l,r); if(r>mid) update(now<<1|1,l,r); } void modify(int now,int l,int r,int x){ if(tree[now].l>=l&&tree[now].r<=r||tree[now].v==x){ tree[now].v=x; return; } if(tree[now].v) tree[now<<1].v=tree[now].v,tree[now<<1|1].v=tree[now].v,tree[now].v=0; int mid=(tree[now].l+tree[now].r)>>1; if(l<=mid) modify(now<<1,l,r,x); if(r>mid) modify(now<<1|1,l,r,x); if(tree[now<<1].v==tree[now<<1|1].v) tree[now].v=tree[now<<1].v; } void print(int now){ if(tree[now].v){ for(int i=tree[now].l;i<=tree[now].r;i++) printf("%c",tree[now].v+'a'-1); return; } print(now<<1);print(now<<1|1); } int main(){ ljb(); scanf("%d%d",&n,&m); scanf("%s",str+1); build(1,1,n); for(int i=1;i<=m;i++){ scanf("%d%d%d",&l,&r,&opt); for(int j=1;j<=28;j++) f[j]=0; update(1,l,r); if(opt){ for(int j=1;j<=26;j++){ if(f[j]){ modify(1,l,l+f[j]-1,j); l+=f[j]; } } } else{ for(int j=26;j>=1;j--){ if(f[j]){ modify(1,l,l+f[j]-1,j); l+=f[j]; } } } } print(1); return 0; }
T2 matrix

神仙dp。只能%%%tqr

#include<bits/stdc++.h> using namespace std; const int maxn=1e6+7; const int N=5505; const int mod=998244353; int c[N][N]; int x,y; int n,m; void pre(){ c[0][0]=1; for(int i=1;i<=m;i++){ c[i][0]=1; for(int j=1;j<=i;j++) c[i][j]=(1LL*c[i][j-1]*(i-j+1))%mod; } } int l[maxn],r[maxn]; int f[N][N]; void dp(){ f[1][0]=1; for(int i=1;i<=m;i++){ for(int j=0;j<=r[i];j++){ if(i-j<l[i]) break; f[i][j]=1LL*f[i][j]*c[i-j-l[i-1]][l[i]-l[i-1]]%mod; f[i+1][j]=(f[i+1][j]+f[i][j])%mod; f[i+1][j+1]=(f[i+1][j+1]+1LL*f[i][j]*(r[i+1]-j)%mod)%mod; } } cout<<f[m][n]; } int main(){ freopen("matrix.in","r",stdin); freopen("matrix.out","w",stdout); scanf("%d%d",&n,&m); pre(); for(int i=1;i<=n;i++){ scanf("%d%d",&x,&y); l[x]++;r[y]++; } for(int i=1;i<=m;i++){ l[i]+=l[i-1]; r[i]+=r[i-1]; } dp(); return 0; }
T3 big
暴力很好想,用前缀和可以减少一个n的复杂度。
关键是题目中的那个式子如何转化,就是前移n位然后把之前的位补到后面,不知道这样解释对不对??:
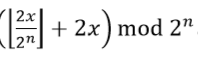
正解是在trie树上贪心的dfs,以后看到异或,还是可以往trie树上想一想。
代码如下:

#include<bits/stdc++.h> using namespace std; const int maxn=1e6+7; int a[maxn];//原来的数组 int suf[maxn];//后缀xor和 int b[maxn];//改变之后的和 int n,m; int change(int x){ return (((x<<1)/(1<<n))+(x<<1))%(1<<n); } int tr[maxn*2][2]; int rt=1; int tot; void trie(int x){ int rt=0; for(int i=n-1;i>=0;i--){ int cur=(x>>i)&1;//取出当前位 if(!tr[rt][cur]) tr[rt][cur]=++tot; rt=tr[rt][cur]; } } int maxx,cnt; void dfs(int now,int dep,int ans){ if(dep==-1){ if(ans>maxx){ maxx=ans; cnt=1; } else if(ans==maxx) cnt++; return; } if(tr[now][0]&&tr[now][1]){ dfs(tr[now][0],dep-1,ans); dfs(tr[now][1],dep-1,ans); } else if(tr[now][1]!=0) dfs(tr[now][1],dep-1,ans+(1<<dep)); else dfs(tr[now][0],dep-1,ans+(1<<dep)); } int main(){ freopen("big.in","r",stdin); freopen("big.out","w",stdout); scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) scanf("%d",&a[i]); for(int i=m;i>=0;i--) suf[i]=suf[i+1]^a[i]; for(int i=0;i<=m;i++){ a[i]=a[i]^a[i-1]; b[i]=change(a[i]); } for(int i=0;i<=m;i++) b[i]=b[i]^suf[i+1]; for(int i=0;i<=m;i++) trie(b[i]); dfs(0,n-1,0); printf("%d\n%d\n",maxx,cnt); return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号