P4139 上帝与集合的正确用法 （扩展欧拉定理）

题目链接

对于这道题，我们需要知道一个规律即扩展欧拉定理：

 

 对于题目中的式子：

 

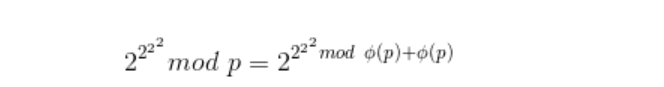
这个式子满足递归的性质，所以我们可以一直递归求出，递归的终止条件是模数为1。所以一直快速幂就可以求了。

先线筛求出1-1e7以内的φ值，然后用以上规律解决。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e7+7;
int phi[maxn];
int not_prime[maxn];
int prime[maxn];
int cnt;
int vis[maxn];
int n,mo;
void euler(){
    phi[1]=1;
    for(int i=2;i<=maxn;i++){
        if(!not_prime[i]){
            prime[++cnt]=i;
            phi[i]=i-1;
        } 
        for(int j=1;j<=cnt;j++){
            if(prime[j]*i>maxn) break;
            not_prime[prime[j]*i]=true;
            if(i%prime[j]) phi[i*prime[j]]=phi[i]*(prime[j]-1);
            else{
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            } 
        }
    }
}
long long ksm(long long x,int n,int mod){
    long long base=1;
    while(n){
        if(n&1) base=base*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return base;
}
long long work(int p){
    if(p==1) return 0;
    else return ksm(2,work(phi[p])+phi[p],p);
} 
int main(){
    euler();
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&mo);
        printf("%lld\n",work(mo));
    }
    return 0;
}