洛谷P1471 方差 线段树维护区间方差

题目链接

偶然在讨论里看到这道题，就进来了。

看了一下发现是求区间的平均数及方差，所以肯定是要用线段树来维护的。区间平均数好求，直接求一遍区间和再除以区间长度就是了。

关键是区间方差的问题，做这题的时候还忘了方差是什么东西，真的sb，初中数学白学了。其实这样也比较可以。

手推一下就能够比较容易地发现，维护方差，还需要维护区间平方和，首先求出当前区间的平均数，再操作一番。

具体如下，非常简单，用HF的话来说就是小学水平。

 

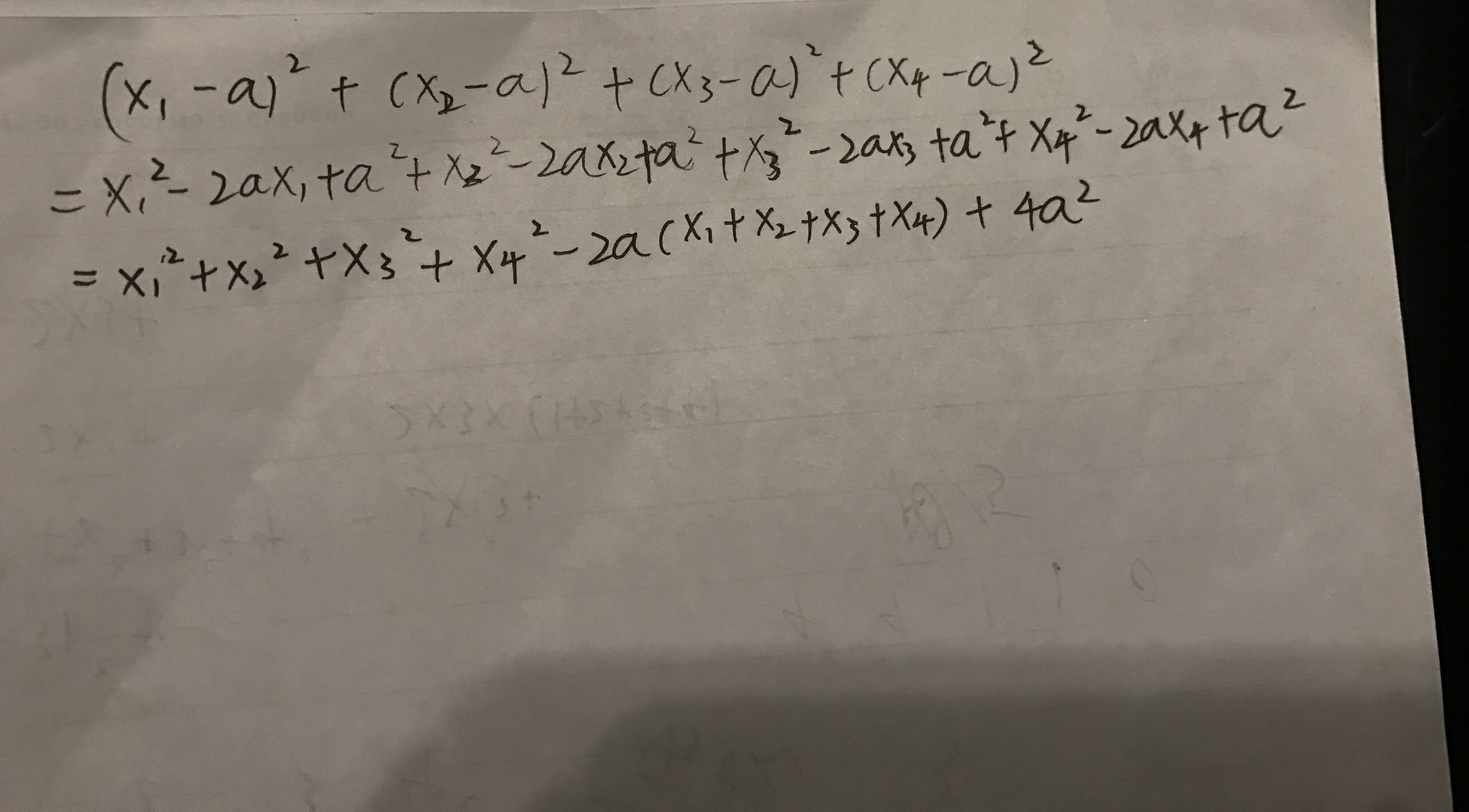
就是你把那求方差的过程看成整个区间都减一个数，然后结果就是原来区间的平方和-2平均数区间和+区间长度平均数的平方，同样，区间修改维护平方和也是这样。那么求方差的时候，就要先让整个区间减去平均数，求一遍平方和/区间长度，最后加上原来减去的平均数值，以便区间中的数值不会改变。

还有一个就是我们下放标记的时候必须先修改平方和，因为它要用到之前区间和的值，顺序还是要有的，不能xjb乱放。

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+7;
int n,m;
double a[maxn];
int opt,l,r;
double v;
struct node{
    int l,r;
    double lazy;
    double sum1,sum2;
}tree[maxn*4];
void build(int now,int l,int r){
    tree[now].l=l,tree[now].r=r;
    if(l==r){
        tree[now].sum1=a[l];
        tree[now].sum2=a[l]*a[l];
        return;
    }
    int mid=(l+r)>>1;
    build(now<<1,l,mid);
    build(now<<1|1,mid+1,r);
    tree[now].sum1=tree[now<<1].sum1+tree[now<<1|1].sum1;
    tree[now].sum2=tree[now<<1].sum2+tree[now<<1|1].sum2;
}
void pushdown(int now){
    if(tree[now].lazy){
        tree[now<<1].sum2+=(tree[now<<1].r-tree[now<<1].l+1)*(tree[now].lazy)*(tree[now].lazy)+2*(tree[now].lazy)*(tree[now<<1].sum1);
        tree[now<<1|1].sum2+=(tree[now<<1|1].r-tree[now<<1|1].l+1)*(tree[now].lazy)*(tree[now].lazy)+2*(tree[now].lazy)*(tree[now<<1|1].sum1);
        tree[now<<1].sum1+=(tree[now<<1].r-tree[now<<1].l+1)*tree[now].lazy;
        tree[now<<1|1].sum1+=(tree[now<<1|1].r-tree[now<<1|1].l+1)*tree[now].lazy;
        tree[now<<1].lazy+=tree[now].lazy;
        tree[now<<1|1].lazy+=tree[now].lazy;
        tree[now].lazy=0;
    }
}
void update(int now,int l,int r,double v){
    if(tree[now].l>=l&&tree[now].r<=r){
        tree[now].sum2+=(tree[now].r-tree[now].l+1)*v*v+2*v*(tree[now].sum1);
        tree[now].sum1+=(tree[now].r-tree[now].l+1)*v;
        tree[now].lazy+=v;
        return;
    }
    pushdown(now);
    int mid=(tree[now].l+tree[now].r)>>1;
    if(l<=mid) update(now<<1,l,r,v);
    if(r>mid) update(now<<1|1,l,r,v);
    tree[now].sum1=tree[now<<1].sum1+tree[now<<1|1].sum1;
    tree[now].sum2=tree[now<<1].sum2+tree[now<<1|1].sum2;
}
double query1(int now,int l,int r){
    if(tree[now].l>=l&&tree[now].r<=r) return tree[now].sum1;
    pushdown(now);
    double val=0;
    int mid=(tree[now].l+tree[now].r)>>1;
    if(l<=mid) val+=query1(now<<1,l,r);
    if(r>mid) val+=query1(now<<1|1,l,r);
    return val;
}
double query2(int now,int l,int r){
    if(tree[now].l>=l&&tree[now].r<=r) return tree[now].sum2;
    pushdown(now);
    double val=0;
    int mid=(tree[now].l+tree[now].r)>>1;
    if(l<=mid) val+=query2(now<<1,l,r);
    if(r>mid) val+=query2(now<<1|1,l,r);
    return val;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%lf",&a[i]);
    build(1,1,n);
    for(int i=1;i<=m;i++){
        scanf("%d",&opt);
        if(opt==1){
            scanf("%d%d%lf",&l,&r,&v);
            update(1,l,r,v);
        }
        if(opt==2){
            scanf("%d%d",&l,&r);
            printf("%.4lf\n",query1(1,l,r)/(r-l+1));
        }
        if(opt==3){
            scanf("%d%d",&l,&r);
            double change=query1(1,l,r)/(r-l+1);
            update(1,l,r,-change);
            printf("%.4lf\n",query2(1,l,r)/(r-l+1));
            update(1,l,r,change);
        }
    }
    return 0;
}