绝对是全网最好的Splay 入门详解——洛谷P3369&BZOJ3224: Tyvj 1728 普通平衡树 包教包会
平衡树是什么东西想必我就不用说太多了吧。
百度百科:
一个月之前的某天晚上,yuli巨佬为我们初步讲解了Splay,当时接触到了平衡树里的旋转等各种骚操作,感觉非常厉害。而第二天我调Splay的模板竟然就搞了一天,最后还是失败告终,只能CV了事,而Splay也成了我心中的一个心结,一直没法解决。在西安集训的时候也没有去自己亲自地把Splay调出来AC,后来又面临期末考试,直到今天,我再一次地尝试将Splay调出来,又花了2个多小时的时间。这个过程是非常痛苦的,翻了无数篇博客,看了无数题解,我才勉强打出了适合我自己的Splay模板。

看到AC的那一瞬间,心里面是五味杂陈,虽然我是如此垃圾,现在我才自己将这样的模板A掉,但看了网上那么多篇博客,学了很多种方法,但适合我自己的我却花了很长的时间才完成。所以我希望写一篇博客,真真正正地手把手教大家Splay(仅仅是模板),让学Splay的神犇们少走一些弯路。这也许就是我这一篇博客的意义所在吧。
来看洛谷的题面:

基本操作简介:
维护的数组:
size[]:子树的大小
cnt[]:某个节点出现的次数
fa[]:某个节点它的父亲节点
val[]:某个节点对应的权值
lc[]:该节点的左儿子
rc[]:该节点的右儿子
变量:
root 根
tot 统计节点数
函数:
clear:用于删除节点时的清空
代码如下:
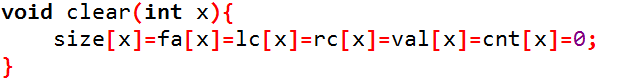
push:随时需要更新
代码如下:
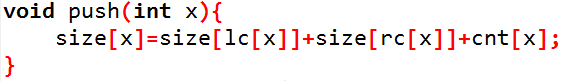
我们看到插入,删除等操作,就自然而然地想到用平衡树来解决它,而要完成这样的操作,最重要的核心步骤就是旋转。而旋转又分为Zig右旋和Zag左旋
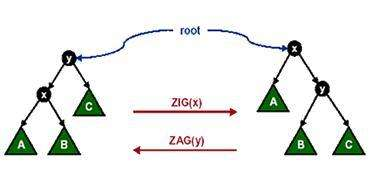
大家看这张图还是比较清晰明确的,其实旋转可以这样理解,一家人,x是儿子,y是x的爸爸,而z是x的爷爷,有一天,一种神奇的力量改变了他们之间的这种关系,本来是儿子的x变成了它本身父亲y的父亲,而x的爷爷z就变成了x的新父亲。
按照上图,我们将x右旋,x的父亲y此时就变成了它的右儿子。而x本身已经有一个右儿子了,这个右儿子就通过旋转变成了y的左儿子。而左旋的话就同理可得,x的父亲y就变成了他的左儿子,而本身x的左儿子又变成了它原来父亲y的右儿子。这样在旋转过后整个结构仍然满足之前的平衡性质。
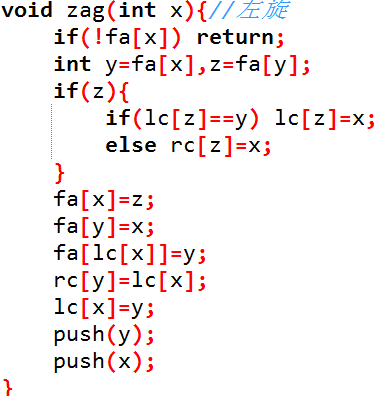
旋转zig和zag的代码我都习惯分开写,两个的实现起来都差不多,比较好理解。
zig:

zag同zig也是基本相同:
zig和zag在这里已经讲明白了,那么就应该是核心Splay伸展操作了,也是基于zig和zag之上的,就是将我们要操作的那个点x旋转到指定节点(一般是根节点为保证复杂度)的位置。但我们在这里还需要有一些分类讨论。
首先看x的爷爷z是否已经在我们需要的节点上了,如果在的话,x就只需要旋转两次就可以到指定节点的下方。
那么我们现在就需要看一看x,y,z之间的相对位置。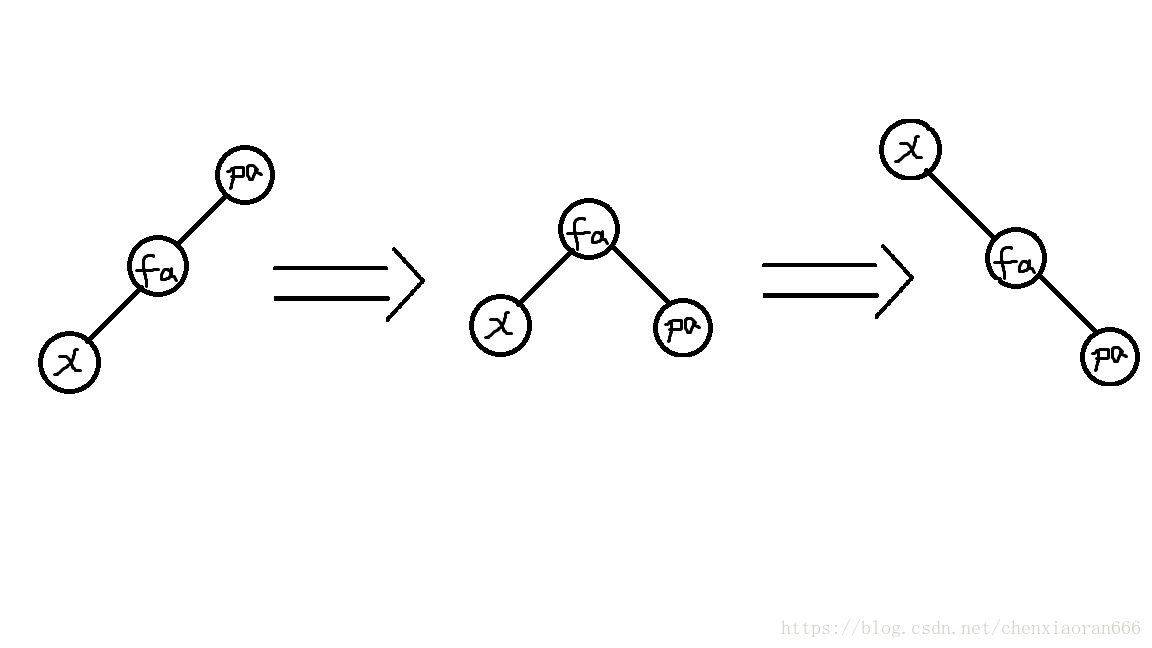
1:若x是y的左儿子,y是z的左儿子(借用某大佬博客中的图片,感谢)
此时x,y,z在同一条直线上,所以我们要将x和y都旋转zig-zig
代码片段:

2:若x是y的右儿子,y是z的右儿子,即也是在同一条直线上,那么结果和第一种情况相同,只不过应该是zag-zag
同样给出代码:
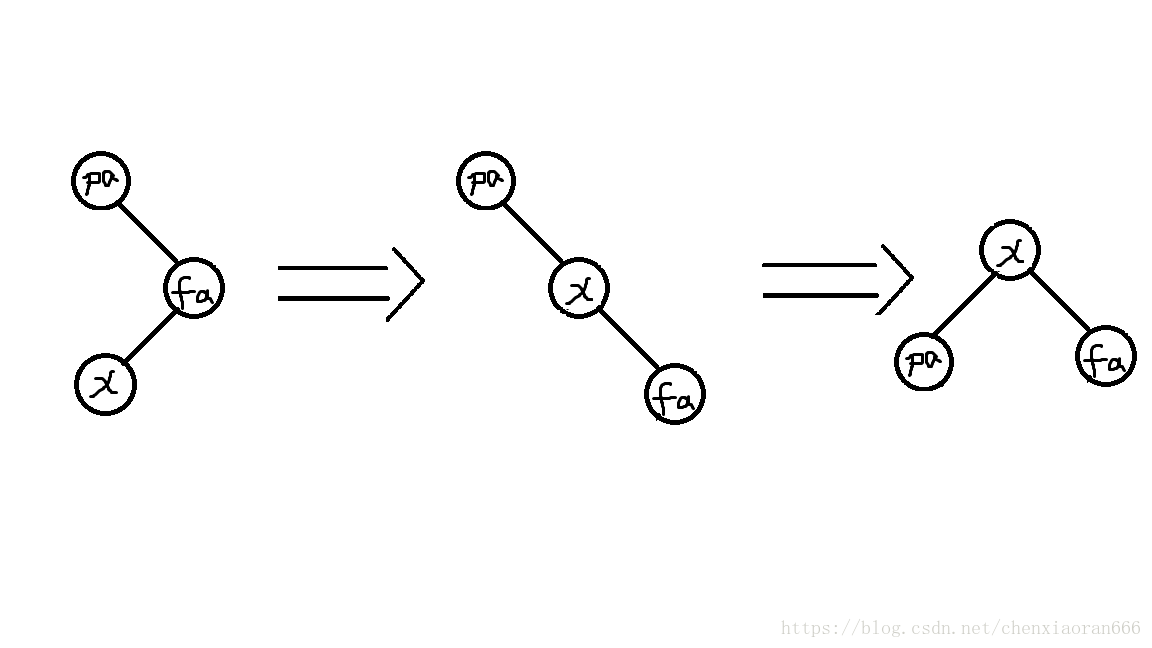
那当它们不再同一条直线上,又怎么办呢,图示已经给出来了,我们只需要转x就可以了。
显而易见的引出第三种情况x是y的右儿子,y是z的左儿子,所以我们先将x左旋,变成y的左儿子,再将x右旋到目标节点,这样就是zag-zig,代码如下:

第4中情况也就可以类比然后得出,x是y的左儿子,y是z的右儿子,这样就将x先右旋,再将其左旋,即为zig-zag操作,代码如下:

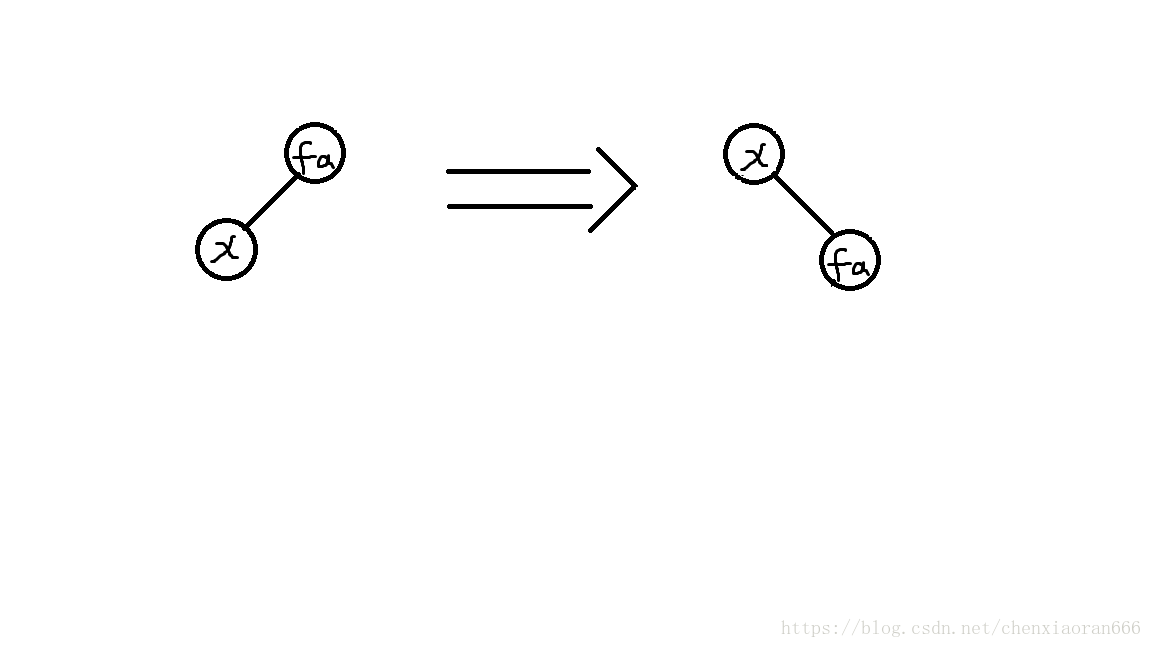
需要转两次的4种情况讲完了,那转一次就更简单了,如上图,y是目标节点,x转一下就登天了,如果x是y的右儿子,那就左旋,反之,如果是左儿子,那么他就右旋。
代码如下:

如果最后连x的父亲都是0了,那它肯定就转到根节点上了,大功告成!
完整代码如下:

接下来是insert操作:
如果此时根节点为空,说明树也为空,那么就新开一个节点,当前的节点就作为根节点。
代码如下:

此时如果已经有元素在树上了,我们就需要按照平衡树的性质(左儿子的值小于父亲,右儿子的值大于父亲)将其插入进去。从根节点开始往下找合适的位置。最后千万不要忘了更新。
我们需要插入的值如果之前已经有了,那么我们只需要将这个值出现的次数加1即可。再把这个节点旋到根。代码如下:

按一般的情况,就是以平衡树的性质插入即可。如果走到了空节点,将它插入,还需要更新其父亲的信息
维护两个变量,也可以理解为在树上的两个指针,一个是指向当前节点(从根节点开始),另一个是指向当前节点的父亲,最后还要将操作的节点旋到根。
代码如下:

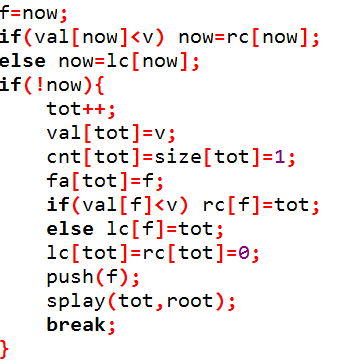
完整的insert操作如下:
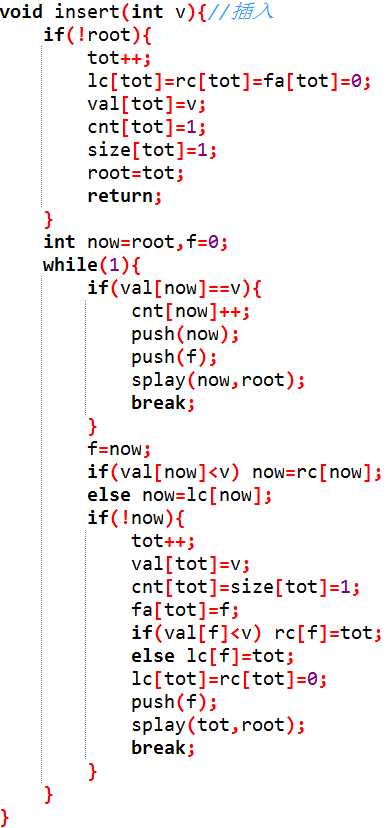
好啦,接下来又是与插入操作对应的删除操作。
先求出该点对应的排名,因为之后会用到,此时x已经在根节点root上了。
如果这个点早就出现过,即cnt[x]>1,那么cnt[x]-1,直接删除就得了。
代码如下:

针对一些特殊的情况,还需要繁杂的分类讨论,这是删除操作的难点所在。
1:没有左儿子和右儿子,孤身一人,直接清空即可。
代码如下:
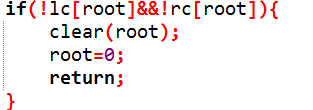
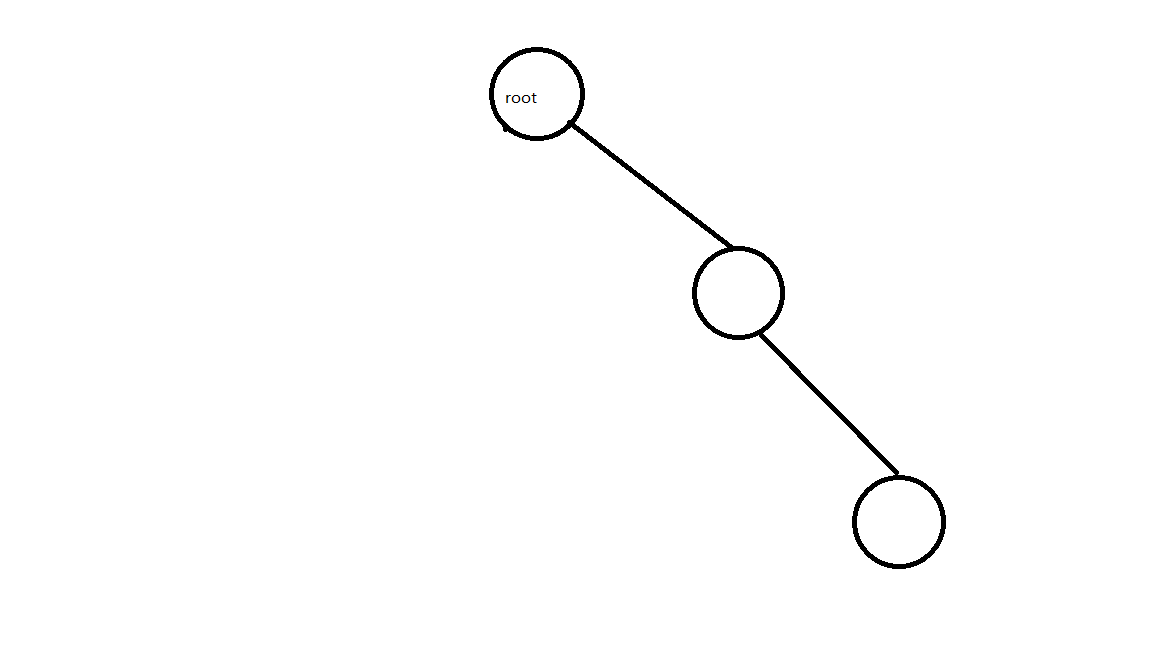
2:没有左儿子,更新现在的根节点,删去老的根节点即可。
现在的树就是这样:
代码如下:
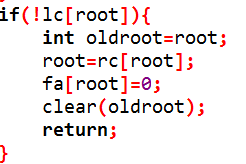
3:没有右儿子,同2操作。
树是这样的:
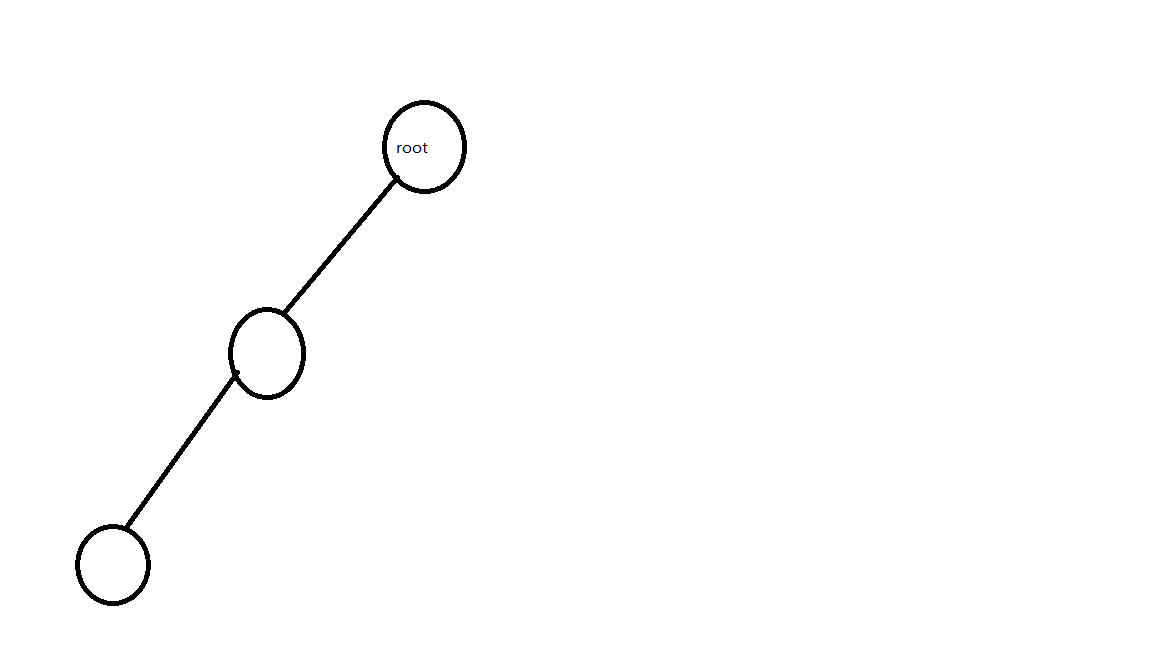
代码如下:

一般的情况:
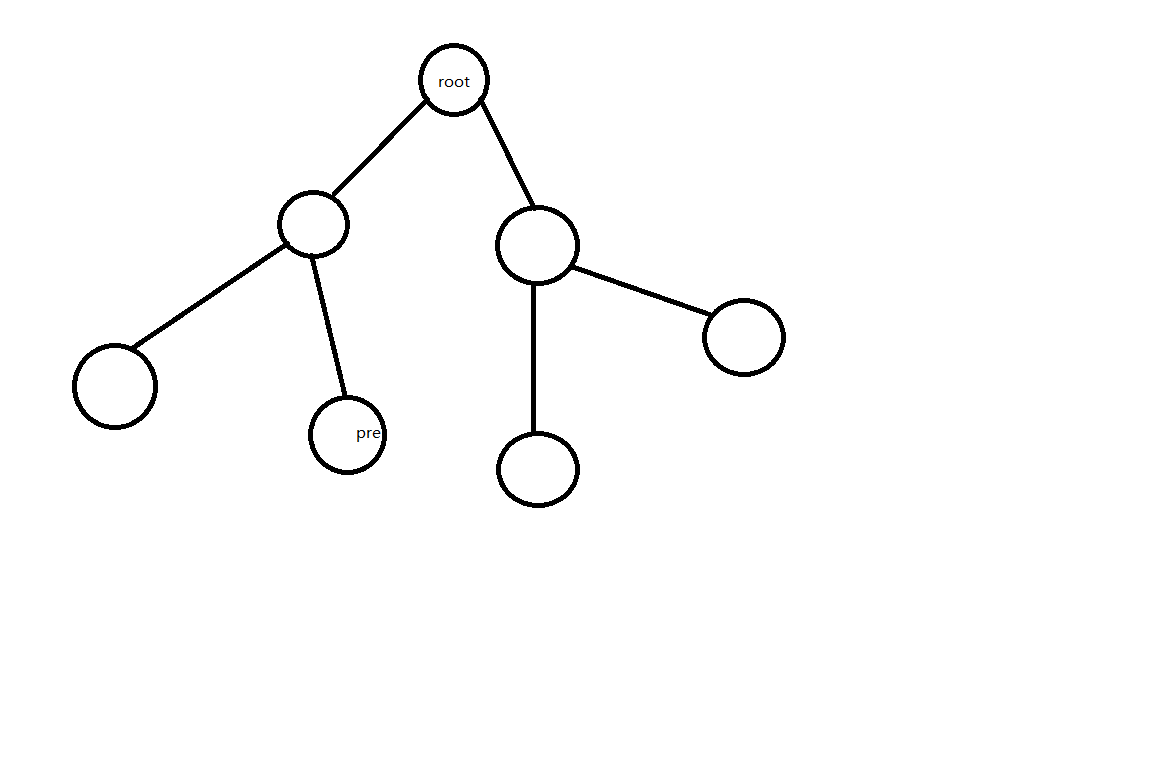
在这种情况下,我们需要求出根节点的前驱(小于x点中最大的数)然后将前驱节点Splay到根,这样也同时能够保证树的平衡。整棵右子树就成了新的根的右儿子,这样的话原来的老根就排除出外了,直接clear即可。
代码如下:
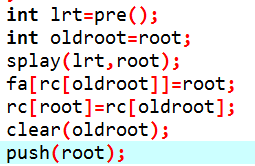
删除操作的完整版:

查询排名:
这其实很好的利用到了平衡树的性质。我们同样用一个now指针在树上找,如果值比它小就走左子树,大的话就往右子树走,走的时候累加左子树的size大小。若有多个重复的数,还要在排名中加上该数出现的次数。
代码如下图所示:

查找排名为k的数实际上就与排名的查询一个道理,但细节上也有不同。
如果当前点有左子树,并且x比左子树的大小小的话,即向左子树寻找;
否则,向右子树寻找:先判断是否有右子树,然后记录右子树的大小以及当前点的大小(都为权值),用于判断是否需要继续向右子树寻找。如果当前点有左子树,并且x比左子树的大小小的话,即向左子树寻找。

前驱和后继的查找道理就非常简单,我的代码也简单易懂,直接把查询的点插入作为根节点,从根节点向下找,最后删除即可。

Splay其实还是很简单的是不是。
完整代码见下方:
#include<bits/stdc++.h> using namespace std; const int maxn=1e6+7; int fa[maxn],lc[maxn],rc[maxn],val[maxn],cnt[maxn],size[maxn]; int root,tot; int n,opt,x; void clear(int x){ size[x]=fa[x]=lc[x]=rc[x]=val[x]=cnt[x]=0; } void push(int x){ size[x]=size[lc[x]]+size[rc[x]]+cnt[x]; } void zig(int x){//右旋 if(!fa[x]) return; int y=fa[x],z=fa[y]; if(z){ if(lc[z]==y) lc[z]=x; else rc[z]=x; } fa[x]=z; fa[y]=x; fa[rc[x]]=y; lc[y]=rc[x]; rc[x]=y; push(y); push(x); } void zag(int x){//左旋 if(!fa[x]) return; int y=fa[x],z=fa[y]; if(z){ if(lc[z]==y) lc[z]=x; else rc[z]=x; } fa[x]=z; fa[y]=x; fa[lc[x]]=y; rc[y]=lc[x]; lc[x]=y; push(y); push(x); } void splay(int x,int rt){//伸展 rt=fa[rt]; int y,z; while(fa[x]!=rt){ y=fa[x]; z=fa[y]; if(z&&z!=rt){ if(lc[z]==y&&lc[y]==x){ zig(y); zig(x); } else if(lc[z]==y&&rc[y]==x){ zag(x); zig(x); } else if(rc[z]==y&&lc[y]==x){ zig(x); zag(x); } else{ zag(y); zag(x); } } else if(lc[y]==x){ zig(x); } else{ zag(x); } } if(!fa[x]) root=x; } void insert(int v){//插入 if(!root){ tot++; lc[tot]=rc[tot]=fa[tot]=0; val[tot]=v; cnt[tot]=1; size[tot]=1; root=tot; return; } int now=root,f=0; while(1){ if(val[now]==v){ cnt[now]++; push(now); push(f); splay(now,root); break; } f=now; if(val[now]<v) now=rc[now]; else now=lc[now]; if(!now){ tot++; val[tot]=v; cnt[tot]=size[tot]=1; fa[tot]=f; if(val[f]<v) rc[f]=tot; else lc[f]=tot; lc[tot]=rc[tot]=0; push(f); splay(tot,root); break; } } } int find1(int v){//查询v的排名 int now=root,ans=0; while(1){ if(v<val[now]) now=lc[now]; else{ ans+=size[lc[now]]; if(v==val[now]){ splay(now,root); return ans+1; } ans+=cnt[now]; now=rc[now]; } } } int find2(int x){//查询排名为x数的值 int now=root; while(1){ if(lc[now]&&x<=size[lc[now]]) now=lc[now]; else{ int ans=size[lc[now]]+cnt[now]; if(ans>=x) return val[now]; x-=ans; now=rc[now]; } } } int pre(){//查找前驱和后继 int now=lc[root]; while(rc[now]) now=rc[now]; return now; } int nex(){ int now=rc[root]; while(lc[now]) now=lc[now]; return now; } void del(int x){//删除某个数 find1(x); if(cnt[root]>1){ cnt[root]--; push(root); return; } if(!lc[root]&&!rc[root]){ clear(root); root=0; return; } if(!lc[root]){ int oldroot=root; root=rc[root]; fa[root]=0; clear(oldroot); return; } if(!rc[root]){ int oldroot=root; root=lc[root]; fa[root]=0; clear(oldroot); return; } int lrt=pre(); int oldroot=root; splay(lrt,root); fa[rc[oldroot]]=root; rc[root]=rc[oldroot]; clear(oldroot); push(root); } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d%d",&opt,&x); if(opt==1) insert(x); if(opt==2) del(x); if(opt==3) printf("%d\n",find1(x)); if(opt==4) printf("%d\n",find2(x)); if(opt==5) insert(x),printf("%d\n",val[pre()]),del(x); if(opt==6) insert(x),printf("%d\n",val[nex()]),del(x); } return 0; }




