模板—割点

终于把割点的模板给调出来了

割点的定义：

在无向连通图中，如果将其中一个点以及所有连接该点的边去掉，图就不再连通，那么这个点就叫做割点（cut vertex / articulation point）。

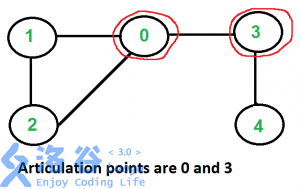
例如，在下图中，0、3是割点，因为将0和3中任意一个去掉之后，图就不再连通。如果去掉0，则图被分成1、2和3、4两个连通分量；如果去掉3，则图被分成0、1、2和4两个连通分量。

 

既然是tarjan求，必然少不了dfn[]和low[]两种数组,定义可以参考其它有关tarjan的博客

而如果一个点是割点，则它满足的性质有

1.如果他是父亲节点，则他的子树大于2个，那他一定是割点

2。如果他是普通节点，那么如果他的后代的low[]比他的时间戳dfn[]小于等于，那么这说明他的后代必须要经过他才能够往上走，如果把它去掉整个图就不联通了。

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+7;
struct node{
    int nxt;
    int to;
}edge[2*maxn];
int head[maxn],cnt,tot;
bool check[maxn];
int cut[maxn];
void add(int x,int y){
    edge[++cnt].nxt=head[x];
    edge[cnt].to=y;
    head[x]=cnt;
}
int n,m,x,y;
int dfn[maxn],low[maxn],sta[maxn],Time;
void dfs(int x,int fa){
    dfn[x]=low[x]=++Time;
    int son=0;//统计以x为根的子树个数 
    for(int i=head[x];i;i=edge[i].nxt){
        int v=edge[i].to;
        if(!dfn[v]){
            dfs(v,fa);
            low[x]=min(low[x],low[v]);
            if(x==fa) son++;
            if(x!=fa&&low[v]>=dfn[x]) check[x]=true;//如果其不是根节点，但是它的孩子能回溯到的最近时间比其大，说明其子必须要经过它，所以去掉他则原图不会联通，所以是割点 
          }
          else low[x]=min(low[x],dfn[v]); //这个非常重要，一定要是和他能走到得点的时间做比较，而不能和它们的low比较，否则可能会搜不到割点 
    }
    if(x==fa&&son>=2) check[fa]=true;//如果节点是根节点并且子树大于2，是割点 
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }
    for(int i=1;i<=n;i++){
        if(!dfn[i]) dfs(i,i);
    } 
    for(int i=1;i<=n;i++){
        if(check[i]) cut[++tot]=i; 
    }
    printf("%d\n",tot);
    sort(cut+1,cut+1+tot);
    for(int i=1;i<=tot;i++) printf("%d ",cut[i]);
    return 0; 
} 

关于代码中还有一个小问题，是关于

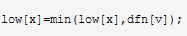
在洛谷上有dalao给出了很好的解释