线段树(3)
hdu 4614 Vases and Flowers
0~n-1的区间,初始值为0,m个操作。
两种操作:
1 X Y 从位置X开始寻找Y个0,如果不足Y个,则寻找尽量多的0,并将他们的值全部修改为1,输出第一个和最后一个修改的1的位置。
2 X Y 输出区间[ X , Y ]内1的个数,并将区间内的1修改为0。
做法:记录区间内1的个数。。关键是第一种操作,ret表示区间[x,n]内0的个数,tmp表示[1,x-1]内0的个数。查询的时候看ls内0的个数是不是大于等于c。

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<string> 5 #include<cstring> 6 #include<algorithm> 7 #include<set> 8 using namespace std; 9 10 #define ULL unsigned long long 11 #define eps 1e-9 12 #define inf 0x3f3f3f3f 13 #define ls i << 1 14 #define rs ls | 1 15 #define md ((ll + rr) >> 1) 16 #define lson ll, md, ls 17 #define rson md + 1, rr, rs 18 #define LL long long 19 #define N 50010 20 #define M 200020 21 #define mod 1000000007 22 23 int sum[N<<2], down[N<<2]; 24 void build(int ll, int rr, int i){ 25 sum[i] = 0, down[i] = -1; 26 if(ll == rr) return ; 27 build(lson), build(rson); 28 } 29 void push_down(int i, int ll, int rr){ 30 if(down[i] != -1){ 31 down[ls] = down[rs] = down[i]; 32 sum[ls] = down[i] ? md - ll + 1 : 0; 33 sum[rs] = down[i] ? rr - md : 0; 34 down[i] = -1; 35 } 36 } 37 void push_up(int i){ 38 sum[i] = sum[ls] + sum[rs]; 39 } 40 void update(int l, int r, int v, int ll, int rr, int i){ 41 if(l == ll && r == rr){ 42 down[i] = v; 43 sum[i] = v ? rr - ll + 1 : 0; 44 return ; 45 } 46 push_down(i, ll, rr); 47 if(r <= md) update(l, r, v, lson); 48 else if(l > md) update(l, r, v, rson); 49 else update(l, md, v, lson), update(md+1, r, v, rson); 50 push_up(i); 51 } 52 int query(int l, int r, int ll, int rr, int i){ 53 if(l == ll && r == rr) 54 return sum[i]; 55 push_down(i, ll, rr); 56 int ret; 57 if(r <= md) ret = query(l, r, lson); 58 else if(l > md) ret = query(l, r, rson); 59 else ret = query(l, md, lson) + query(md + 1, r, rson); 60 push_up(i); 61 return ret; 62 } 63 64 int qR(int c, int ll, int rr, int i){ 65 if(ll == rr) 66 return ll; 67 push_down(i, ll, rr); 68 int ret; 69 int tmp = md - ll + 1 - sum[ls]; 70 if(tmp >= c) 71 ret = qR(c, lson); 72 else ret = qR(c - tmp, rson); 73 push_up(i); 74 return ret; 75 } 76 int main(){ 77 int cas; 78 //freopen("tt.txt", "r", stdin); 79 scanf("%d", &cas); 80 while(cas--){ 81 int n, m; 82 scanf("%d%d", &n, &m); 83 build(1, n, 1); 84 while(m--){ 85 int op, x, y; 86 scanf("%d%d%d", &op, &x, &y); 87 if(op == 1){ 88 x++; 89 int ret = n - x + 1 - query(x, n, 1, n, 1); 90 int tmp = n - sum[1] - ret; 91 if(ret == 0){ 92 puts("Can not put any one."); continue; 93 } 94 y = min(y, ret); 95 int l = qR(1 + tmp, 1, n, 1); 96 int r = qR(y + tmp, 1, n, 1); 97 update(l, r, 1, 1, n, 1); 98 l--, r--; 99 printf("%d %d\n", l, r); 100 } 101 else{ 102 x++, y++; 103 printf("%d\n", query(x, y, 1, n, 1)); 104 update(x, y, 0, 1, n, 1); 105 } 106 } 107 puts(""); 108 } 109 return 0; 110 }
zoj 3299 Fall the Brick
有n个木块,m个板。木块从上往下掉,覆盖的范围是[l, r],板的高度h不一样,能够接到木块的范围是[L, R],问每块板上能接多少木块。
做法:离散化,先确定每个区间的id,然后线段树区间更新。最后再做一次query。

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<string> 5 #include<cstring> 6 #include<algorithm> 7 #include<ctime> 8 #include<cstdlib> 9 #include<queue> 10 using namespace std; 11 12 #define ULL unsigned long long 13 #define eps 1e-9 14 #define inf 0x3f3f3f3f 15 #define ls i << 1 16 #define rs ls | 1 17 #define md ((ll + rr) >> 1) 18 #define lson ll, md, ls 19 #define rson md + 1, rr, rs 20 #define LL long long 21 #define mod 1000000007 22 #define N 100020 23 #define M 800020 24 25 LL ans[N], a[N<<2]; 26 int add[N<<4], id[N<<4]; 27 void push_down(int i){ 28 if(id[i]){ 29 id[ls] = id[rs] = id[i]; 30 id[i] = 0; 31 } 32 if(add[i]){ 33 add[ls] += add[i], add[rs] += add[i]; 34 add[i] = 0; 35 } 36 } 37 void update(int l, int r, int u, int ll, int rr, int i){ 38 if(l == ll && r == rr){ 39 if(u) id[i] = u; 40 else add[i]++; 41 return ; 42 } 43 push_down(i); 44 if(r <= md) update(l, r, u, lson); 45 else if(l > md) update(l, r, u, rson); 46 else update(l, md, u, lson), update(md + 1, r, u, rson); 47 } 48 49 void query(int ll, int rr, int i){ 50 if(ll == rr){ 51 ans[id[i]] += (LL)(a[rr+1] - a[rr]) * add[i]; 52 return; 53 } 54 push_down(i); 55 query(lson), query(rson); 56 } 57 struct query{ 58 int L, R, H, id; 59 void input(int i){ 60 scanf("%d%d%d", &L, &R, &H); 61 id = i; 62 } 63 bool operator < (const query &b) const { 64 return H < b.H; 65 } 66 }q[N]; 67 int L[N], R[N]; 68 int main(){ 69 int n, m; 70 while(scanf("%d%d", &n, &m) != EOF){ 71 memset(ans, 0, sizeof ans); 72 memset(id, 0, sizeof id); 73 memset(add, 0, sizeof add); 74 int cnt = 0; 75 for(int i = 1; i <= n; ++i){ 76 scanf("%d%d", &L[i], &R[i]); 77 a[++cnt] = L[i], a[++cnt] = R[i]; 78 } 79 for(int i = 1; i <= m; ++i){ 80 q[i].input(i); 81 a[++cnt] = q[i].L, a[++cnt] = q[i].R; 82 } 83 sort(a + 1, a + 1 + cnt); 84 cnt = unique(a + 1, a + 1 + cnt) - a - 1; 85 sort(q + 1, q + 1 + m); 86 for(int i = 1; i <= m; ++i){ 87 int l = lower_bound(a + 1, a + 1 + cnt, q[i].L) - a; 88 int r = lower_bound(a + 1, a + 1 + cnt, q[i].R) - a; 89 update(l, r - 1, q[i].id, 1, cnt, 1); 90 } 91 for(int i = 1; i <= n; ++i){ 92 int l = lower_bound(a + 1, a + 1 + cnt, L[i]) - a; 93 int r = lower_bound(a + 1, a + 1 + cnt, R[i]) - a; 94 update(l, r - 1, 0, 1, cnt, 1); 95 } 96 query(1, cnt, 1); 97 for(int i = 1; i <= m; ++i){ 98 printf("%lld\n", ans[i]); 99 } 100 puts(""); 101 } 102 return 0; 103 }
CF 266E More Queries to Array...
给你一串数,编号从1~n,进行m次操作。(1 <= n , m <= 10 ^ 5 )
= L R X 区间【L,R】上的数设为X
?L R K 输出 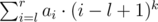 。
。
做法:对询问进行二项式展开,得到 segma(j = 0, k)[C(k, j) * (1 - l)^(k - j)] * segma(i = l, r)[ai * i^j]。。由于0 <= k <= 5,对于后面部分可以直接开6棵线段树保存。然后前面部分预处理出组合数,询问的时候乘上就好了。

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <cmath> 6 #include <queue> 7 #include <stack> 8 using namespace std; 9 10 #define LL long long 11 #define eps 1e-8 12 #define inf 0x3f3f3f3f 13 #define MP make_pair 14 #define N 100020 15 #define M 400020 16 #pragma comment(linker, "/STACK:1024000000,1024000000") 17 #define Pi acos(-1.0) 18 #define mod 1000000007 19 #define ls (i << 1) 20 #define rs (ls | 1) 21 #define md ((ll + rr) >> 1) 22 #define lson ll, md, ls 23 #define rson md + 1, rr, rs 24 25 LL c[10][10], s[N][6]; 26 void init(){ 27 c[0][0] = 1; 28 for(int i = 1; i <= 6; ++i){ 29 c[i][0] = 1; 30 for(int j = 1; j <= i; ++j) 31 c[i][j] = c[i-1][j] + c[i-1][j-1]; 32 } 33 for(int i = 0; i < N; ++i){ 34 for(int j = 0; j < 6; ++j){ 35 s[i][j] = 1; 36 for(int k = 0; k < j; ++k) 37 s[i][j] = s[i][j] * i % mod; 38 } 39 } 40 for(int i = 1; i < N; ++i) 41 for(int j = 0; j < 6; ++j) 42 s[i][j] = (s[i][j] + s[i-1][j]) % mod; 43 } 44 LL sum[N<<2][6]; 45 int down[N<<2]; 46 void f(int v, int ll, int rr, int i){ 47 down[i] = v; 48 for(int j = 0; j < 6; ++j) 49 sum[i][j] = (s[rr][j] - s[ll-1][j] + mod) % mod * v % mod; 50 } 51 void push_down(int i, int ll, int rr){ 52 if(~down[i]){ 53 f(down[i], lson); 54 f(down[i], rson); 55 down[i] = -1; 56 } 57 } 58 void push_up(int i){ 59 for(int j = 0; j < 6; ++j) 60 sum[i][j] = (sum[ls][j] + sum[rs][j]) % mod; 61 } 62 void build(int ll, int rr, int i){ 63 down[i] = -1; 64 if(ll == rr){ 65 int v; 66 scanf("%d", &v); 67 for(int j = 0; j < 6; ++j) 68 sum[i][j] = (s[rr][j] - s[rr-1][j] + mod) % mod * v % mod; 69 return ; 70 } 71 build(lson), build(rson); 72 push_up(i); 73 } 74 75 void update(int l, int r, int v, int ll, int rr, int i){ 76 if(l == ll && r == rr){ 77 f(v, ll, rr, i); 78 return ; 79 } 80 push_down(i, ll, rr); 81 if(r <= md) update(l, r, v, lson); 82 else if(l > md) update(l, r, v, rson); 83 else update(l, md, v, lson), update(md + 1, r, v, rson); 84 push_up(i); 85 } 86 LL query(int l, int r, int p, int v, int ll, int rr, int i){ 87 if(l == ll && r == rr){ 88 LL ret = 0, tmp = 1; 89 for(int j = v; j >= 0; --j){ 90 //printf("%lld\n", sum[i][j]); 91 ret = (ret + sum[i][j] * c[v][j] % mod * tmp % mod + mod) % mod; 92 tmp = tmp * (1 - p) % mod; 93 // printf("%lld\n", ret); 94 } 95 return ret; 96 } 97 push_down(i, ll, rr); 98 LL ret; 99 if(r <= md) ret = query(l, r, p, v, lson); 100 else if(l > md) ret = query(l, r, p, v, rson); 101 else ret = (query(l, md, p, v, lson) + query(md + 1, r, p, v, rson)) % mod; 102 push_up(i); 103 return ret; 104 } 105 int main(){ 106 init(); 107 int n, m; 108 scanf("%d%d", &n, &m); 109 build(1, n, 1); 110 while(m--){ 111 int L, R, k; 112 char ch[5]; 113 scanf("%s%d%d%d", &ch, &L, &R, &k); 114 if(ch[0] == '=') 115 update(L, R, k, 1, n, 1); 116 else printf("%I64d\n", query(L, R, L, k, 1, n, 1)); 117 } 118 return 0; 119 }
hdu 4417 Super Mario
长为n的序列,q次询问,每次输出[l, r]内小于h的个数
做法:离散化,将询问排序。线段树搞一下。(将初始序列排序,询问再排序,用树状数组也能搞,而且更快)

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<string> 5 #include<cstring> 6 #include<algorithm> 7 #include<set> 8 #include<queue> 9 #include <bitset> 10 using namespace std; 11 12 #define ULL unsigned long long 13 #define eps 1e-9 14 #define inf 0x3f3f3f3f 15 #define ls i << 1 16 #define rs ls | 1 17 #define md ((ll + rr) >> 1) 18 #define lson ll, md, ls 19 #define rson md + 1, rr, rs 20 #define LL long long 21 #define N 100100 22 #define M 200200 23 #define mod 2015 24 #define MP make_pair 25 #define PB push_back 26 27 int sum[N<<4]; 28 void update(int p, int ll, int rr, int i){ 29 if(ll == rr){ 30 sum[i]++; 31 return ; 32 } 33 if(p <= md) update(p, lson); 34 else update(p, rson); 35 sum[i] = sum[ls] + sum[rs]; 36 } 37 int query(int l, int r, int ll, int rr, int i){ 38 if(l == ll && r == rr) 39 return sum[i]; 40 if(r <= md) return query(l, r, lson); 41 if(l > md) return query(l, r, rson); 42 return query(l, md, lson) + query(md + 1, r, rson); 43 } 44 struct node{ 45 int p, h, id; 46 node(int p = 0, int h = 0, int id = 0) : p(p), h(h), id(id) {} 47 bool operator < (const node &b) const{ 48 return p < b.p; 49 } 50 }L[N], R[N]; 51 int cnt, a[N], b[N<<1], qL[N], qR[N]; 52 int Hash(int v){ 53 return (int)(lower_bound(b + 1, b + 1 + cnt, v) - b); 54 } 55 void debug(){ 56 for(int i = 1; i <= cnt; ++i) 57 printf("%d ", b[i]); 58 cout << endl; 59 } 60 int main(){ 61 int cas, kk = 0; 62 scanf("%d", &cas); 63 while(cas--){ 64 int n, m; 65 scanf("%d%d", &n, &m); 66 cnt = 0; 67 for(int i = 1; i <= n; ++i){ 68 scanf("%d", &a[i]); 69 b[++cnt] = a[i]; 70 } 71 for(int i = 1; i <= m; ++i){ 72 int l, r, h; 73 scanf("%d%d%d", &l, &r, &h); 74 l++, r++; 75 L[i] = node(l, h, i); 76 R[i] = node(r, h, i); 77 b[++cnt] = h; 78 } 79 sort(b + 1, b + 1 + cnt); 80 cnt = unique(b + 1, b + 1 + cnt) - b - 1; 81 sort(L + 1, L + 1 + m); 82 sort(R + 1, R + 1 + m); 83 // debug(); 84 memset(sum, 0, sizeof sum); 85 int j = 1, k = 1; 86 for(int i = 1; i <= n; ++i){ 87 while(L[j].p == i){ 88 int p = Hash(L[j].h); 89 // printf("%d\n", p); 90 qL[L[j].id] = query(1, p, 1, cnt, 1); 91 j++; 92 } 93 int p = Hash(a[i]); 94 update(p, 1, cnt, 1); 95 while(R[k].p == i){ 96 int p = Hash(R[k].h); 97 qR[R[k].id] = query(1, p, 1, cnt, 1); 98 k++; 99 } 100 } 101 printf("Case %d:\n", ++kk); 102 for(int i = 1; i <= m; ++i){ 103 printf("%d\n", qR[i] - qL[i]); 104 } 105 } 106 return 0; 107 }




