三点坐标，求三角形面积 ，一个点判断是否在三角形中 c++

给定二维平面中的三个坐标点，求三角形面积

通过一波向量推导和余弦函数公式，能推导出来

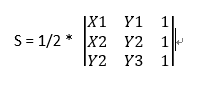
s = |(x1y2 - x1y3 - x2y1 + x3y1 + x2y3 - x3y2) / 2|

这最后的公式公式记不住，还是记上面的行列式吧

 

以下是c++实现的代码

#include <iostream>
#include <cmath>
using namespace std;

struct point {
    double x, y;
    point(double x,double y) {
        point::x = x;
        point::y = y;
    }
};

double triangle(point a, point b, point c) {
    return fabs((a.x * b.y - a.x * c.y - b.x * a.y + c.x * a.y + b.x * c.y - c.x * b.y)/ 2.0);
}

int main() {
    point a(0,0);
    point b(1,0);
    point c(0.5,0.5);
    cout << triangle(a,b,c);
    return 0;
}

 

判断一个点是否在这个三角形中

思路：若该点在三角形中，则 S(ABC) =  S(ABP) + S(ACP) + S(BCP)

实现代码

#include <iostream>
#include <cmath>
using namespace std;

struct point {
    double x, y;
    point(double x, double y) {
        point::x = x;
        point::y = y;
    }
};

double triangle(point a, point b, point c) {
    return fabs((a.x * b.y - a.x * c.y - b.x * a.y + c.x * a.y + b.x * c.y - c.x * b.y) / 2.0);
}

bool in_triangle(point a, point b, point c, point p) {
    double s = triangle(a, b, c);
    double s1 = triangle(a, b, p);
    double s2 = triangle(a, c, p);
    double s3 = triangle(b, c, p);
    return s == (s1 + s2 + s3) ? true : false;
}

int main() {
    point a(0, 0);
    point b(1, 0);
    point c(0.5, 0.5);
    point p(1,1);
    cout << in_triangle(a,b,c,p);
    return 0;
}