【动态规划】背包问题----多重背包

问题描述

acwing 多重背包

多重背包基础版

要点

1.每种物品只能使用si次
2.总体积不超过V
3.总价值最大

分析

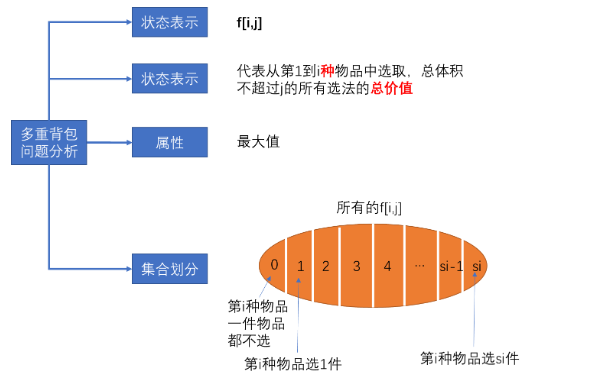
按照第i个物品选取的个数进行集合划分

第i种物品1件物品都不选 f[i - 1][j]
第i种物品选1件 f[i - 1][ j - v[i]] + w[i]
第i种物品选2件 f[i - 1][ j - v[i] * 2] + w[i] * 2
…
第i种物品选si件 f[i - 1][ j - v[i] * si] + w[i] * si

---

问题的属性是最大值，则f[i,j]可以表示如下
f[i,j]=max(f[i−1][j],f[i−1][j−v[i]]+w[i],f[i−1][j−v[i]∗2]+w[i]∗2,f[i−1][j−v[i]∗3]+w[i]∗3,...f[i−1][j−v[i]∗si]+w[i]∗si) (1)
按照之前我们在完全背包问题的经验，我们观察（2）式如下
f[i,j−v[i]]=max(f[i−1][j−v[i]],f[i−1][j−v[i]∗2]+w[i],f[i−1][j−v[i]∗3]+w[i]∗2,...f[i−1][j−v[i]∗(si)]+w[i]∗(si−1),f[i−1][j−v[i]∗(si+1)]+w[i]∗si)(2)

可以看到多了一项，无法进行直接带入。

一维写法（数据较小时）

暴力拆分变成01背包

#include <bits/stdc++.h>

using namespace std;

const int N = 110;

int v[N], w[N], s[N]; //体积  价值  个数
int f[N];

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1;i <= n; i++) scanf("%d%d%d", &v[i], &w[i], &s[i]);

    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= s[i]; j ++)
            for (int k = m; k >= v[i]; k --)
                f[k] = max(f[k], f[k - v[i]] + w[i]);

    printf ("%d\n", f[m]);

    return 0;
}

多重背包二进制优化版

分析

例如si = 17，则si = 2⁰ + 2¹ + 2² + 2³ + 2
给2^k的各个项及C赋予系数{0， 1}可以表示出 0~si 的所有情况
例如对于 0~17 中的14，可以表示为：
14 = 0* 2⁰ + 1* 2¹ + 1* 2² + 1* 2³ + 0*2

如此之下，我们就无需在第三层循环中枚举k，而是可以将si分成 log₂si 堆物品，每堆物品 2^k 件物品，最后一堆为C件物品，将每堆物品视为一件物品，这样每"件”物品就有了新的体积和价值（也就是组成它的所有物品的体积之和和价值之和）。将每种物品都做这样的分解，这样我们就可以得到总共 Nlog₂si “件”新物品，这些每件只能取一个或者0个。这就把原来的多重背包问题转换成了新物品的01背包问题。这样就降低了时间复杂度。

代码

#include <bits/stdc++.h>

using namespace std;

const int N = 25000; //2000 * log2 2000

int n, m;
int v[N], w[N];
int f[N];
int cnt = 0; //cnt记录共有多少组物体

int main()
{
    scanf ("%d%d", &n, &m);
    
    for (int i = 1; i <= n; i ++)
    {
        int a, b, s; //体积  价值  个数
        scanf ("%d%d%d", &a, &b, &s);

        int k = 1;
        while (k <= s)
        {
            //按照二进制的形式分组
            cnt ++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2; 
        }
        //不能按照二进制分组的物体数量单独划分为一组（补上最后的C）
        if (s > 0) 
        {
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    //分组完后等同于 01背包
    for (int i = 1; i <= cnt; i ++)
        for (int j = m; j >= v[i]; j --)
            f[j] = max (f[j], f[j - v[i]] + w[i]);
            
    printf ("%d\n", f[m]);
    
    return 0;
}

多重背包滑动窗口优化版