【动态规划】背包问题----完全背包

题目描述

acwing 完全背包

要点

1.每种物品可选无数次
2.总体积不超过V
3.总价值最大

分析

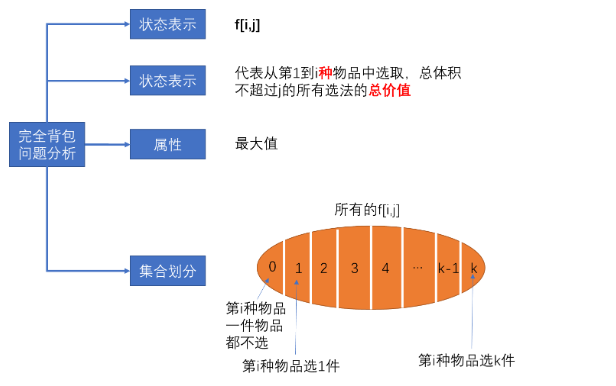
按照第i个物品选几个将集合进行划分

第i种物品1件物品都不选 f[i - 1][j]
第i种物品选1件 f[i - 1][ j - v[i]] + w[i]
第i种物品选2件 f[i - 1][ j - v[i] * 2] + w[i] * 2
…
第i种物品选k件 f[i - 1][ j - v[i] * k] + w[i] * k

---

问题的属性是最大值，则f[i,j]可以表示如下

f[i,j]=max(f[i−1][j],f[i−1][j−v[i]]+w[i],f[i−1][j−v[i]∗2]+w[i]∗2,f[i−1][j−v[i]∗3]+w[i]∗3,...f[i−1][j−v[i]∗k]+w[i]∗k) (1)

我们观察（2）式如下
f[i,j−v[i]]=max(f[i−1][j−v[i]],f[i−1][j−v[i]∗2]+w[i],f[i−1][j−v[i]∗3]+w[i]∗2,...f[i−1][j−v[i]∗k]+w[i]∗(k−1))(2)

为何正序

数组中元素可以重复使用

代码

与01背包问题的基础问题一样，f[i,j]也可以使用一维数组进行表示

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N];

int main()
{
    int n, m;
    scanf ("%d%d", &n, &m);

    for (int i = 1; i <= n; i ++) scanf ("%d%d", &v[i], &w[i]);

    for (int i = 1; i <= n; i ++) 
        for (int j = v[i]; j <= m; j ++)
            f[j] = max (f[j], f[j - v[i]] + w[i]);

    printf ("%d\n", f[m]);

    return 0;
}