理科男

题目描述：

            对于给定的分数 A / B，求其在 K 进制下是有限小数还是循环小数。如果是有限小数，求小数点后的位数；如果是循环小数，则求混循环部分和循环节的长度又分别是多少。 
注意，循环节指的是最短循环节，且混循环部分的长度也指最短。

样例：

       input：

                3
　             1 8 10
                17 99 10
                 217 990 10

       output：        

                 3 0
                 0 2
                 1 2

题解：及其毒瘤的数学题（然而被大佬嘲讽不懂初中数论QAQ）

           结论：循环节长度=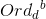           非循环节长度=n

                      其中，对于此题而言，b为k，d为B/C，C为B中所有约数中满足其质因数属于K中最大的那个数。n为尽量大的一个正整数使得d mod K^n==1

           (mmmmmp)

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<set>
#include<queue>
#include<ctime>
#define MAXN 200005
#define ll long long
#define maxn 15
#define maxs 1000005
#define inf 1e9
#define eps 1e-9
using namespace std;
inline char gc() {
    static char now[1<<16],*S,*T;
    if (T==S) {
        T=(S=now)+fread(now,1,1<<16,stdin);
        if (T==S) return EOF;
    }
    return *S++;
}
inline ll readlong() {
    ll x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') {
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') {
        x*=10;
        x+=ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline int read() {
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') {
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') {
        x*=10;
        x+=ch-'0';
        ch=getchar();
    }
    return x*f;
}
void putint(long long t) {
    int ans[40]= {0};
    for(; t; t/=10)ans[++ans[0]]=t%10;
    for(; ans[0]; ans[0]--)putchar('0'+ans[ans[0]]);
    putchar('\n');
}
ll a,b,k;
ll gcd(ll a,ll b){
    if(b==0){
        return a;
    }
    return gcd(b,a%b);
}
ll phi(ll x){
    ll y=x;
    for(int i=2;(ll)i*i<=x;i++){
        if(x%i==0){
            y=y/i*(i-1);
            do{
                x/=i;
            }while(x%i==0);
        }        
    }
    if(x>1){
        y=y/x*(x-1);
    }
    return y;
}
ll mul(ll a,ll b,ll p){
    ll c=0;
    for(;b;b>>=1,a=(a<<1)%p){
        if(b&1){
            c=(c+a)%p;
        }
    }
    return c;
}
ll pw(ll a,ll n,ll p){
    ll v=1;
    for(;n;n>>=1,a=mul(a,a,p)){
        if(n&1){
            v=mul(v,a,p);
        }
    }
    return v;
}
ll cal(ll A,ll B){
     ll x=phi(B);
     ll y=x;
     for(int i=2;(ll)i*i<=x;i++){
         if(x%i==0){
             while(y%i==0&&pw(A,y/i,B)==1){
                 y/=i;
             }
             do{
                 x/=i;
             }while(x%i==0);
         }
     }
     if(x>1&&pw(A,y/x,B)==1){
         y/=x;
     }
     return y;
}
int main(){
    int T=read();
    while(T--){
        a=readlong();
        b=readlong();
        k=readlong();
        ll g=gcd(a,b);
        a/=g;
        b/=g;
        int a1=0;
        while(1){
            ll x=gcd(b,k);
            if(x==1){
                break;
            }
            b/=x;
            ++a1;
        }
        printf("%d %lld\n",a1,b==1?0ll:cal(k,b));
    }

    return 0;
}