【机器学习】--机器学习之朴素贝叶斯从初始到应用
一、前述
机器学习算法中,有种依据概率原则进行分类的朴素贝叶斯算法,正如气象学家预测天气一样,朴素贝叶斯算法就是应用先前事件的有关数据来估计未来事件发生的概率。
二、具体
1、背景--贝叶斯定理引入
对于两个关联事件(非独立事件)A和B,同时发生的概率为:P(AB)=P(A|B)P(B)=P(B|A)P(A),所以把公式变形后可得:
贝叶斯定理,他是朴素贝叶斯算法的基础,就是下面的这个公式:

现在我们来把这个式子扩充一下:假设B由很多个独立事件组成,或者说,B由很多个属性组成B1,B2...Bn他们相互独立,那上面的式子成了这个样子:
也就是说我们把P(B|A)替换成了P(B1|A)P(B2|A)...P(Bn|A),上面的式子也很容易看出是成立的。我们把上面的公式先记住。其实我学的时候一直在纠结这么明显的式子究竟会起什么作用。
上面公式起作用的前提是假设特征和特征之间是独立的。因此这就是朴素贝叶斯的中朴素一词的来源。
2、案例一
对于垃圾邮件案例来说:
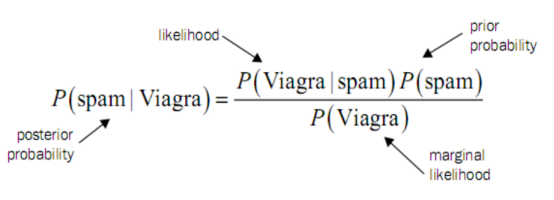
说明:P(spam)是先验概率。
P(spam|Viagra)是后验概率。
构建频率表:
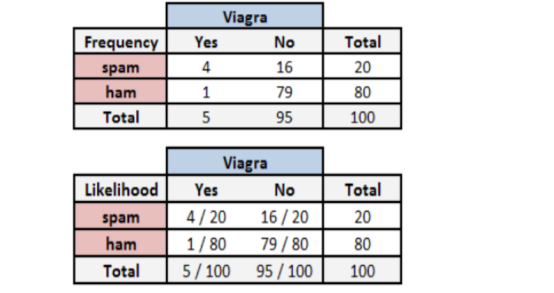
求解:
P(垃圾邮件|Viagra)=P(Viagra|垃圾邮件)*P(垃圾邮件)/P(Viagra)=(4/20)*(20/100)/(5/100)=0.8
结论:
因此,如果电子邮件含有单词Viagra,那么该电子邮件是垃圾邮件的概率为80%。所以,任何含有单词Viagra的消息都需要被过滤掉。
拓展一:假设特征和特征之间是独立的。
当有更多的特征时,则有如下公式:
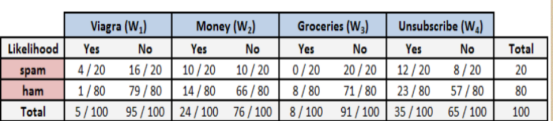
分别求解垃圾邮件概率和非垃圾邮件概率:

分母可以先忽略它,垃圾邮件的总似然为:
• (4/20)*(10/20)*(20/20)*(12/20)*(20/100)=0.012
• 非垃圾邮件的总似然为:
• (1/80)*(66/80)*(71/80)*(23/80)*(80/100)=0.002
• 将这些值转换成概率,我们只需要一步得到垃圾邮件概率为
85.7%
拓展二:假设文章中包含了4个单词的邮件呢?
• 我们可以计算垃圾邮件的似然如下:
• (4/20)*(10/20)*(0/20)*(12/20)*(20/100)=0
• 非垃圾邮件的似然为:
• (1/80)*(14/80)*(8/80)*(23/80)*(80/100)=0.00005
• 因此该消息是垃圾邮件的概率为0/(0+0.00005)=0
• 该消息是非垃圾邮件的概率为0.00005/(0+0.00005)=1
• 问题出在Groceries这个单词,所有单词Grogeries有效抵消或否决了所有其他的证据。
解决方法:
拉普拉斯估计本质上是给频率表中的每个计数加上一个较小的数,这样就保证了每一类中每个特征发生概率非零。
• 通常情况下,拉普拉斯估计中加上的数值设定为1,这样就保证每一类特征的组合至少在数据中出现一次。
• 然后,我们得到垃圾邮件的似然为:
• (5/24)*(11/24)*(1/24)*(13/24)*(24/108)=0.0004
• 非垃圾邮件的似然为:
• (2/84)*(15/84)*(9/84)*(24/84)*(84/108)=0.0001
• 这表明该消息是垃圾邮件的概率为80%,是非垃圾邮件的概率为20%。
3、案例二
让我以一个例子加以说明,假设有这样一个数据集(本例来自朴素贝叶斯分类器的应用),
症状(A1) 职业(A2) 疾病(B)
打喷嚏 护士 感冒
打喷嚏 农夫 过敏
头痛 建筑工人 脑震荡
头痛 建筑工人 感冒
打喷嚏 教师 感冒
头痛 教师 脑震荡
那么一个打喷嚏的建筑工人是感冒还是没感冒呢?根据贝叶斯定理,
P(感冒|打喷嚏x建筑工人) = P(打喷嚏x建筑工人|感冒) x P(感冒) / P(打喷嚏x建筑工人)
假定”打喷嚏”和”建筑工人”这两个特征是独立的,因此,上面的等式就变成了
P(感冒|打喷嚏x建筑工人) = P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒) / P(打喷嚏) x P(建筑工人) = 0.66 x 0.33 x 0.5 / 0.5 x 0.33 = 0.66
同理,
P(非感冒|打喷嚏x建筑工人) = P(打喷嚏|非感冒) x P(建筑工人|非感冒) x P(非感冒) / P(打喷嚏) x P(建筑工人) = 0.33 x 0.33 x 0.5 / 0.5 x 0.33 = 0.33因为P(感冒|打喷嚏x建筑工人) > P(非感冒|打喷嚏x建筑工人) ,所以我们更愿意相信一个打喷嚏的建筑工人是感冒的。
从上面的例子可以看出,贝叶斯分类的步骤是这样的:


因为我们只需求概率的相对值,所以这里只需计算属性的概率密度值即可。得出结论
假设特征服从多项式分布,连续的特征适合用高斯分布的,

比如鸢尾花数据集,如果是离散的特征,适合用多项式分布。
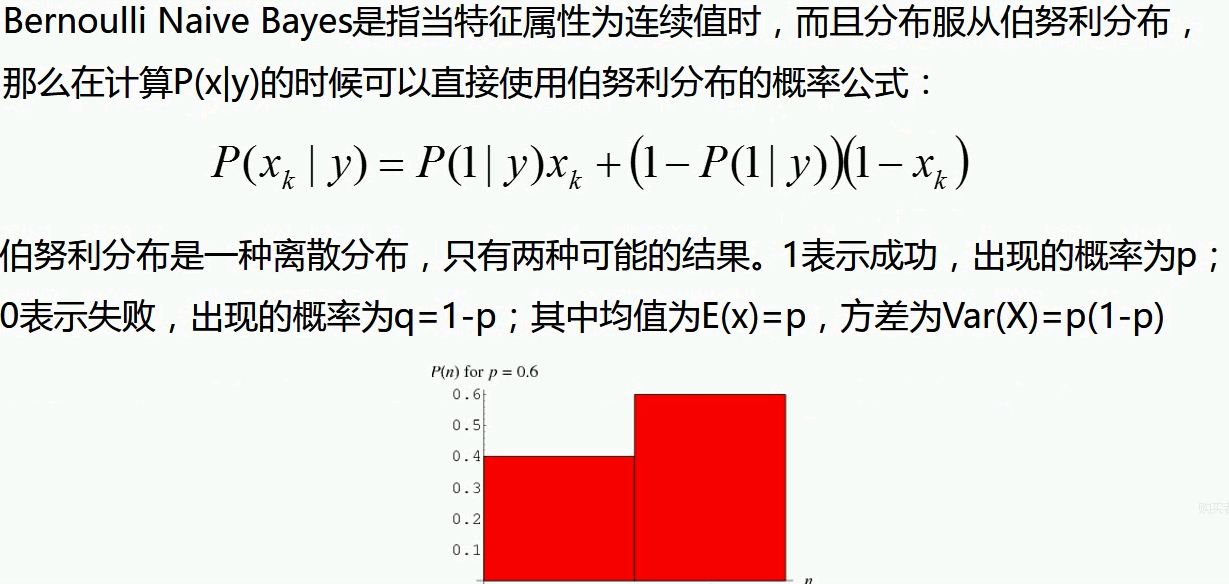
总结:一般三种贝叶斯分类方法分别是高斯、多项式、伯努利
高斯模型:有些特征可能是连续型变量,比如说人的身高,物体的长度,这些特征可以转换成离散型的值,比如如果身高在160cm以下,特征值为1;在160cm和170cm之间,特征值为2;在170cm之上,特征值为3。也可以这样转换,将身高转换为3个特征,分别是f1、f2、f3,如果身高是160cm以下,这三个特征的值分别是1、0、0,若身高在170cm之上,这三个特征的值分别是0、0、1。不过这些方式都不够细腻,高斯模型可以解决这个问题。高斯模型假设这些一个特征的所有属于某个类别的观测值符合高斯分布,
多项式模型:该模型常用于文本分类,特征是单词,值是单词的出现次数。其中,是类别下特征出现的总次数;是类别下所有特征出现的总次数。对应到文本分类里,如果单词word在一篇分类为label1的文档中出现了5次,那么的值会增加5。如果是去除了重复单词的,那么的值会增加1。是特征的数量,在文本分类中就是去重后的所有单词的数量。的取值范围是[0,1],比较常见的是取值为1。
待预测样本中的特征在训练时可能没有出现,如果没有出现,则值为0,如果直接拿来计算该样本属于某个分类的概率,结果都将是0。在分子中加入,在分母中加入可以解决这个问题。
伯努利模型:伯努利模型中,对于一个样本来说,其特征用的是全局的特征。在伯努利模型中,每个特征的取值是布尔型的,即true和false,或者1和0。在文本分类中,就是一个特征有没有在一个文档中出现。如果特征值值为1,那么 如果特征值值为0,那么这意味着,“没有某个特征”也是一个特征。
高斯朴素贝叶斯是利用高斯概率密度来进行分类拟合的,多项式朴素贝叶斯多用于高纬度向量分类,最常用的是文章分类,伯努利朴素贝叶斯一般是针对布尔类型特征值的向量做分类的过程。
4、朴素贝叶斯分类的思想和计算过程






 浙公网安备 33010602011771号
浙公网安备 33010602011771号