【机器学习】--Python机器学习库之Numpy
一、前述
NumPy(Numerical Python的缩写)是一个开源的Python科学计算库。使用NumPy,就可以很自然地使用数组和矩阵。 NumPy包含很多实用的数学函数,涵盖线性代数运算、傅里叶变换和随机数生成等功能。
这个库的前身是1995年就开始开发的一个用于数组运算的库。经过了长时间的发展,基本上成了绝大部分Python科学计算的基础包,当然也包括所有提供Python接口的深度学习框架。
二、具体应用
1、背景--为什么使用Numpy?
a) 便捷:
对于同样的数值计算任务,使用NumPy要比直接编写Python代码便捷得多。这是因为NumPy能够直接对数组和矩阵进行操作,可以省略很多循环语句,其众多的数学函数也会让编写代码的工作轻松许多。
b) 性能:
NumPy中数组的存储效率和输入输出性能均远远优于Python中等价的基本数据结构(如嵌套的list容器)。其能够提升的性能是与数组中元素的数目成比例的。对于大型数组的运算,使用NumPy的确很有优势。对于TB级的大文件,NumPy使用内存映射文件来处理,以达到最优的数据读写性能。
c) 高效:
NumPy的大部分代码都是用C语言写成的,这使得NumPy比纯Python代码高效得多。
当然,NumPy也有其不足之处,由于NumPy使用内存映射文件以达到最优的数据读写性能,而内存的大小限制了其对TB级大文件的处理;此外,NumPy数组的通用性不及Python提供的list容器。因此,在科学计算之外的领域,NumPy的优势也就不那么明显。
2、Numpy的安装
(1) 官网安装。http://www.numpy.org/。
(2) pip 安装。pip install numpy。
(3) LFD安装,针对windows用户http://www.lfd.uci.edu/~gohlke/pythonlibs/。
(4) Anaconda安装(推荐),Anaconda里面集成了很多关于python科学计算的第三方库,主要是安装方便。下载地址:https://www.anaconda.com/download/。
3、numpy 基础:
NumPy的主要对象是同种元素的多维数组。这是一个所有的元素都是一种类型。
在NumPy中维度(dimensions)叫做轴(axes),轴的个数叫做秩(rank)。
NumPy的数组类被称作 ndarray 。通常被称作数组。
常用的ndarray对象属性有:
ndarray.ndim(数组轴的个数,轴的个数被称作秩),
ndarray.shape(数组的维度。这是一个指示数组在每个维度上大小的整数元组。例如一个n行m列的矩阵,它的shape属性将是(2,3),这个元组的长度显然是秩,即维度或者ndim属性),
ndarray.size(数组元素的总个数,等于shape属性中元组元素的乘积)
ndarray.dtype(一个用来描述数组中元素类型的对象,可以通过创造或指定dtype使用标准Python类型。另外NumPy提供它自己的数据类型)。
4、Numpy的数据类型:


三、具体案例
代码一:基本类型标识
import numpy as np a = np.dtype(np.int_) # np.int64, np.float32 … print(a)

int8, int16, int32,int64 可以由字符串’i1’, ‘i2’,’i4’, ‘i8’代替,其余的以此类推。
import numpy as np a = np.dtype('i8') # ’f8’, ‘i4’’c16’,’a30’(30个字符的字符串), ‘>i4’… print (a)
可以指明数据类型在内存中的字节序,’>’表示按大端的方式存储,’<’表示按小端的方式存储,’=’表示数据按硬件默认方式存储。大端或小端存储只影响数据在底层内存中存储时字节的存储顺序,在我们实际使用python进行科学计算时,一般不需要考虑该存储顺序。
代码二:创建数组并查看其属性
import numpy as np a = np.array([[1,2,3], [4, 5, 6]], dtype=int) print(a.shape) # a.ndim, a.size, a.dtype
import numpy as np a = np.array([(1,2,3), (4, 5, 6)], dtype=float) print(a.shape) # a.ndim, a.size, a.dtype

用np.arange().reshape()创建数组:
import numpy as np a = np.arange(10).reshape(2, 5) # 创建2行5列的二维数组, # 也可以创建三维数组, b = np.arange(12).reshape(2,3,2) print(a) print(b)
a = np.array([[[1,2,3], [4, 5, 6], [7, 8, 9]]]) b = np.array([[[1,2,3]], [[4, 5, 6]], [[7, 8, 9]]]) print(a.shape) print(b.shape)


代码三:基本运算
import numpy as np a = np.random.random(6) b = np.random.rand(6) c = np.random.randn(6) print(a-b) # print(a+b),print(a*c) …
print(np.dot(a,b)) #复习矩阵乘法
# Numpy 随机数模块np.random.random, np.random.randn, np.random.rand的比较
(1)rand 生成均匀分布的伪随机数。分布在(0~1)之间
(2)randn 生成标准正态分布的伪随机数(均值为0,方差为1)。
import numpy as np a = np.ones((2,3)) b = np.zeros((2,3)) a*=3 b+=a print(a) print(b)

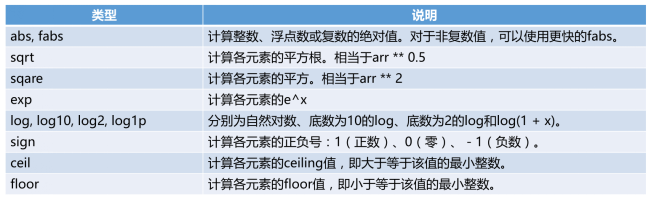
代码四:常用函数






代码五:索引,切片和迭代
import numpy as np a = np.arange(10)**3 print(a) print(a[2:5]) a[:6:2] = -1000 print(a) print(a[ : :-1])
[x:y:z]切片索引,x是左端,y是右端,z是步长,在[x,y)区间从左到右每隔z取值,默认z为1可以省略z参数.
步长的负号就是反向,从右到左取值.
二维数组:
b = np.arange(20).reshape(5,4) print(b) print(b[2,3]) print(b[0:5, 1]) print(b[ : ,1]) print(b[1:3, : ])
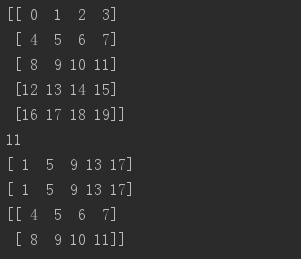
#当少于轴数的索引被提供时,丢失的索引被认为是整个切片
b[-1] #相当于b[-1,:] 最后一行

# b[i] 中括号中的表达式被当作 i 和一系列 : ,来代表剩下的轴。NumPy也允许你使用“点”像 b[i,...] 。
#点 (…)代表许多产生一个完整的索引元组必要的分号。如果x是
#秩为5的数组(即它有5个轴),那么:
x[1,2,…] 等同于 x[1,2,:,:,:],
x[…,3] 等同于 x[:,:,:,:,3],
x[4,…,5,:] 等同 x[4,:,:,5,:].
三维数组:
c = np.arange(12).reshape(2,3,2) print(c) c[1] c[2,1] # 等价于c[2][1] c[2,1,1] # 等价于c[2][1][1]
通过布尔数组索引
f = np.arange(12).reshape(3, 4) print(f) g = f>4 print(g) print(f [g])
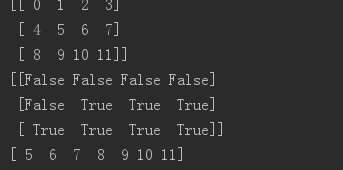
通过迭代取值
h = np.arange(12).reshape(3,4) print(h) for i in h: print(i) for i in h.flat: print(i)
迭代多维数组是就第一个轴而言的:
如果想对每个数组中元素进行运算,我们可以使用flat属性,该属性是数组元素的一个迭代器:
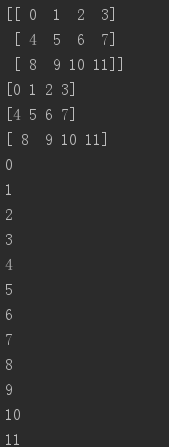
np.flatten()返回一个折叠成一维的数组。但是该函数只能适用于numpy对象,即array或者mat,普通的list列表是不行的。
a = np.array([[1,2], [3, 4], [5, 6]]) print(a.flatten())

代码六:形状操作
ravel(), vstack(),hstack(),column_stack,row_stack, stack, split, hsplit, vsplit
import numpy as np #增加维度 a = np.arange(5) print(a[:, np.newaxis]) print(a[np.newaxis, :]) print(np.tile([1,2], 2))

a = np.arange(10).reshape(2,5) print(a) print(a.ravel()) print(a.resize(5,2)) b = np.arange(6).reshape(2,3) c = np.ones((2,3)) d = np.hstack((b,c)) print(b) print(c) print(d)# hstack:horizontal stack 左右合并

e = np.vstack((b,c)) print(e)# vstack: vertical stack 上下合并 f = np.column_stack((b,c)) g = np.row_stack((b,c)) h = np.stack((b, c), axis=1) # 按行合并 i = np.stack((b,c), axis=0) # 按列合并 j = np.concatenate ((b, c, c, b), axis=0) #多个合并




 浙公网安备 33010602011771号
浙公网安备 33010602011771号