【深度学习篇】--神经网络中的卷积神经网络

一、前述

Convolutional neural networks
 视觉皮层、感受野，一些神经元看线，一些神经元看线的方向，一些神经元有更大的感受野，组合
底层的图案
1998年Yann LeCun等人推出了LeNet-5架构，广泛用于手写体数字识别，包含全连接层和sigmoid
激活函数，还有卷积层和池化层

二、具体原理

1、直观感受：（每一个神经元只看到一部分，并且先看到基本的形状，然后再把相关特征进行组合，只需要局部连接即可）

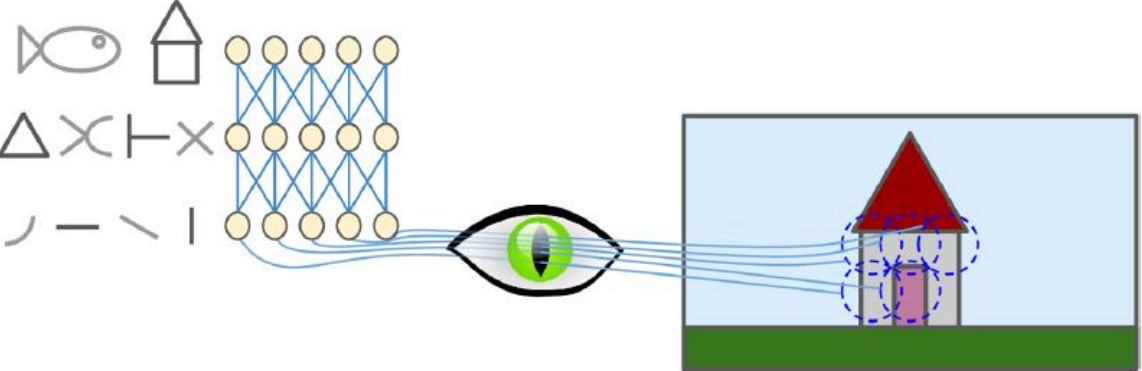
2、卷积层理解

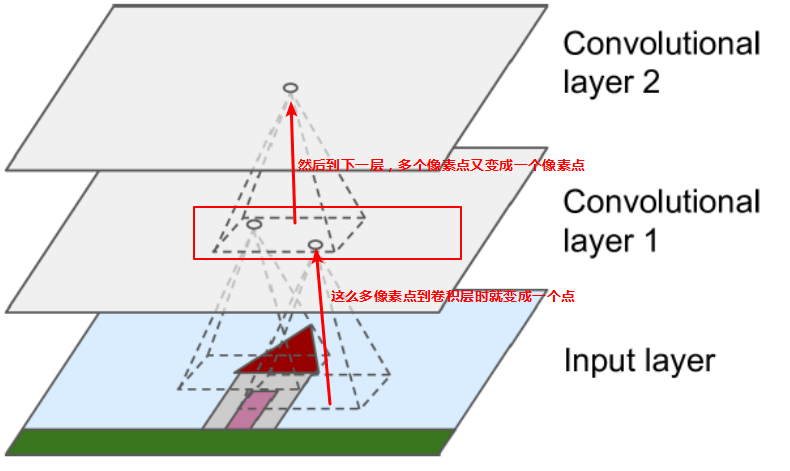
CNN里面最重要的构建单元就是卷积层
神经元在第一个卷积层不是连接输入图片的每一个像素，只是连接它们感受野的像素，以此类推，
第二个卷积层的每一个神经元仅连接位于第一个卷积层的一个小方块的神经元
以前我们做MNIST的时候，把图像变成1D的，现在直接用2D

3、Zero Padding

 

 

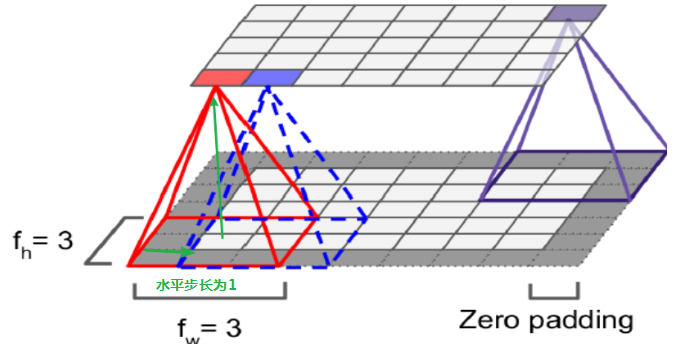
 Zero Padding是一个可选项，加上说明更注重于边缘的像素点

VALID
不适用zero padding，有可能会忽略图片右侧或底下，这个得看stride的设置
SAME
必要会加zero padding，这种情况下，输出神经元个数等于输入神经元个数除以步长 ceil(13/5)=3，当步长为1时卷积完后的长宽一样，像素点一样，维度一样（输入神经元的个数和输出神经元的个数一样）

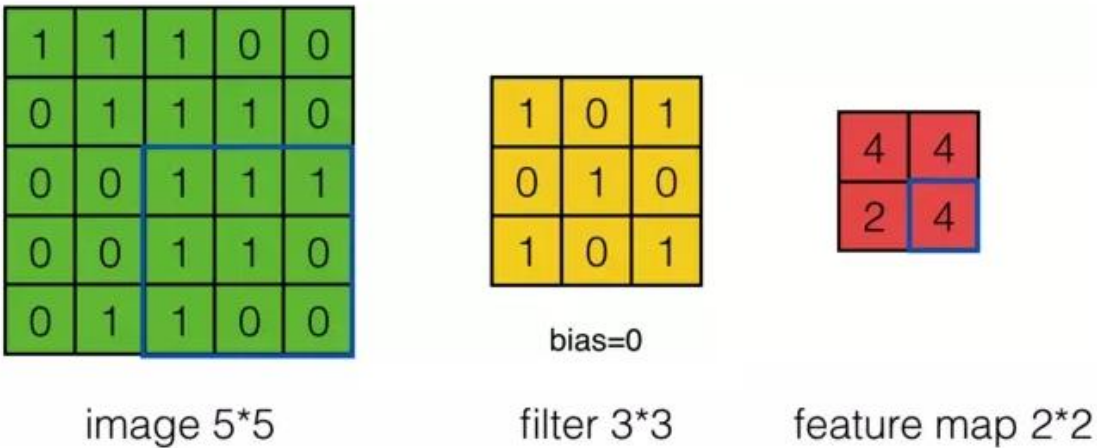
 4、卷积的计算

假设有一个5*5的图像，使用一个3*3的filter（卷积核）进行卷积，想得到一个3*3（没有使用Zero_padding,因为下一层和上一层长宽不一样）的Feature Map。

 

演示如图：

 

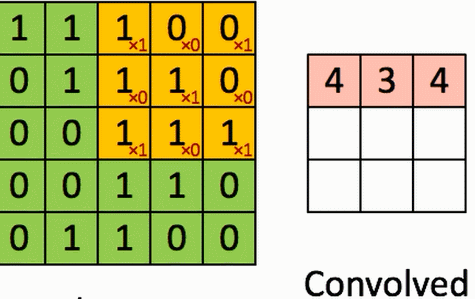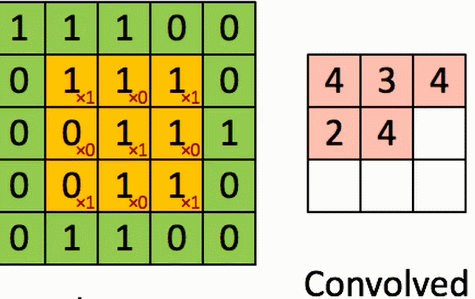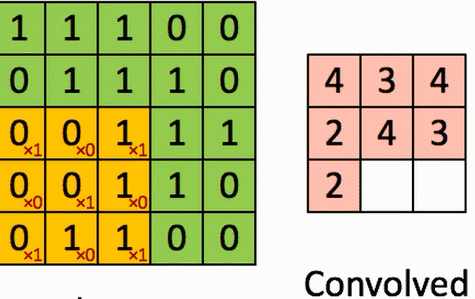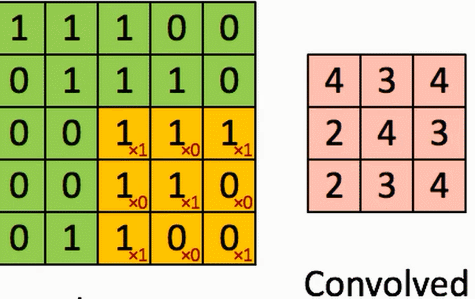
结论：

 

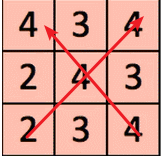
通过3*3的维度可以看到对角线上的大概分布，因为卷积核想保留对角线上的值

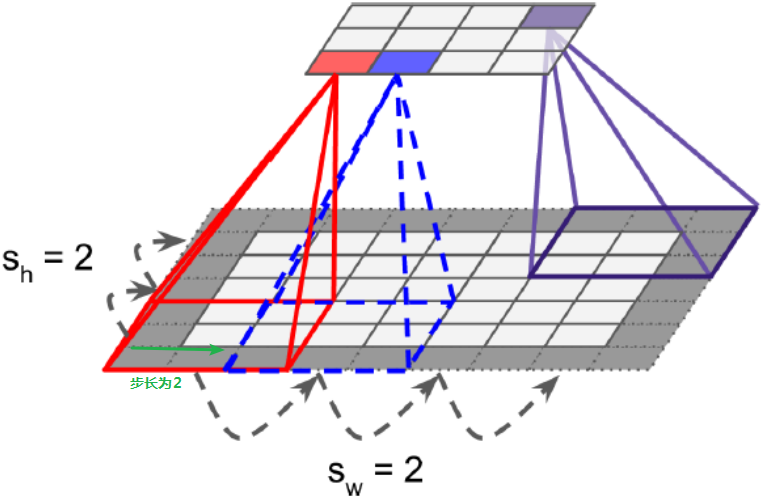
5、当步长为2时（生成的Feacture_map更小了）

举例如下：

 

 

 

 

 

 

6.当多个卷积核时（3D图片使用,3个通道累加，再加上bias偏置项）图示如下：

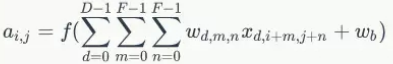
D是深度；F是filter的大小(宽度或高度，两者相同)；
Wd,m,n表示filter的第m行第n列权重；
ad,I,j表示图像的第d层第i行第j列像素；

结论：

在一个卷积层里面可以有多个卷积核，每一个卷积核可以有多个维度

每一个卷积核生成一个Feature_map，因为有两个卷积核，所以生成两个Feacture_Map

 

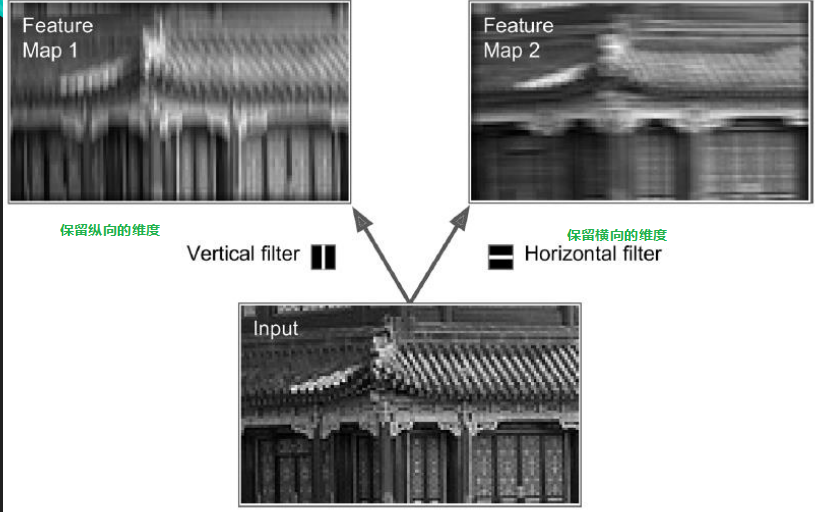
7、卷积核的设置
Vertical line filter 中间列为1，周围列为0
Horizontal line filter 中间行为1，周围行为0

 8、代码演示

import numpy as np
from sklearn.datasets import load_sample_images
import tensorflow as tf
import matplotlib.pyplot as plt


# 加载数据集
# 输入图片通常是3D，[height, width, channels]
# mini-batch通常是4D，[mini-batch size, height, width, channels]
dataset = np.array(load_sample_images().images, dtype=np.float32)
# 数据集里面两张图片，一个中国庙宇，一个花
batch_size, height, width, channels = dataset.shape
print(batch_size, height, width, channels)

# 创建两个filter
# 高，宽，通道，卷积核
# 7, 7, channels, 2
filters_test = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
filters_test[:, 3, :, 0] = 1  # 垂直
filters_test[3, :, :, 1] = 1  # 水平

# filter参数是一个filters的集合
X = tf.placeholder(tf.float32, shape=(None, height, width, channels))
# strides=[1, 2, 2, 1] 中第一最后一个为1，中间对应sh和sw
convolution = tf.nn.conv2d(X, filter=filters_test, strides=[1, 2, 2, 1], padding='SAME')

with tf.Session() as sess:
    output = sess.run(convolution, feed_dict={X: dataset})

plt.imshow(output[1, :, :, 1])  # 绘制第一个图的第二个特征图
plt.show()

 在一个特征图里面，所有的神经元共享一样的参数（weights bias），权值共享