【机器学习】--Kmeans从初识到应用
一.前述
Kmeans算法一般在数据分析前期使用,选取适当的k,将数据分类后,然后分类研究不同聚类下数据的特点。
Kmeans算法是一种无监督的算法。
常用于分组,比如用户偏好。
二.概念及原理
Kmeans原理:
1 随机选取k个中心点
2 遍历所有数据,将每个数据划分到最近的中心点中
3 计算每个聚类的平均值,并作为新的中心点
4 重复2-3,直到这k个中线点不再变化(收敛了),或执行了足够多的迭代。
样本点之间的相似度距离计算:
1.欧氏距离相似度(常用!!!)
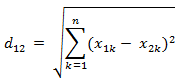
2.Jaccard相似度(用于比较样本之间的相似性,系数值越大表示值越高)

3.余弦相似度
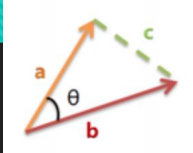

余弦相似度值在[-1,1]之间,值越趋近于1代表越相近,越趋近于-1,代表越相反,接近于0,代表两个向量正交。
常用计算文本相似性!!!将两个文本根据他们词,建立两个向量,计算这两个向量的余弦值,就可以知道两个文本在统计学方法中他们的相似度情况。
4.Pearson相似度
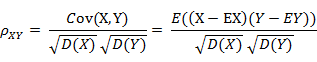
5.相对熵(K-L距离)

总结:
对于高维空间点之间的度量,用欧氏距离。
对于集合度量Jaccard相似度。
对于自然语言处理用余弦相似度。
对于函数度量用Pearson相似度
目标函数:
考虑欧几里得距离的数据,使用误差平方和(Sum of the Squared Error,SSE)作为聚类的目标函数,两次运行K均值产生的两个不同的簇集,我们更喜欢SSE最小的那个。
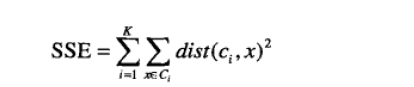
k表示k个聚类中心,ci表示第几个中心,dist表示的是欧几里得距离。
这里有一个问题就是为什么,我们更新质心是让所有的点的平均值,这里就是SSE所决定的。
通俗来说,每个点计算 到所在分配的中心店的距离,然后加和。
随着k的增长损失函数,逐渐递减。肘部法就是计算不同的K,然后计算SSE,求最大的两组即可。
选择一开始下降速度快,后来下降速度慢的。
肘部法图解:

聚类评价方法:

常见的聚类评测指标有纯度和 F 值,其中 F 值更为常用。
F 值的更普适的应用是信息检索的结果,其计算包括了两个指标:召回率(Recall Rate)和准确率(Precision Rate)。
- 召回率的定义为:检索出的相关文档数和文档库中所有的相关文档数的比率,衡量的是检索系统的查全率;
- 准确率的定义为:检索出相关文档数与检索出的文档总数的比率,衡量的是检索系统的查准率;F 值为两者的调和平均值。
以上评估方法都是基于原始数据事先知道一定的标签,但这种似乎并不太常用,所以常用的评估模型的指标是轮廓系数,适用于在一开始不知道标签的情况下。
具体如下:
轮廓系数它结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。
方法:
1,计算样本i到同簇其他样本的平均距离ai。ai 越小,说明样本i越应该被聚类到该簇。将ai 称为样本i的簇内不相似度。
簇C中所有样本的a i 均值称为簇C的簇不相似度。
2,计算样本i到其他某簇Cj 的所有样本的平均距离bij,称为样本i与簇Cj 的不相似度。定义为样本i的簇间不相似度:bi =min{bi1, bi2, ..., bik}
bi越大,说明样本i越不属于其他簇。
3,根据样本i的簇内不相似度a i 和簇间不相似度b i ,定义样本i的轮廓系数:
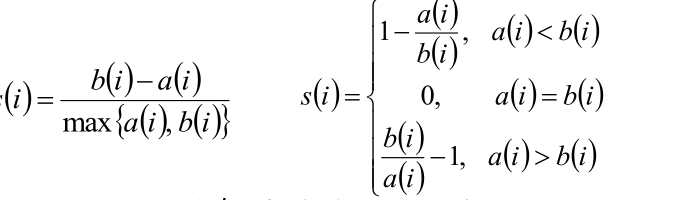
4,判断:
si接近1,则说明样本i聚类合理;
si接近-1,则说明样本i更应该分类到另外的簇;
若si 近似为0,则说明样本i在两个簇的边界上。
结果为负数则可以直接放弃了!!!说明分类的很不好。
二分Kmeans原理:
为了得到k个簇,将所有点的集合分裂成两个簇,从这些簇中选取一个继续分裂,如此下去,直到产生k个簇。
比如要分成5个组,第一次分裂产生2个组,然后从这2个组中选一个目标函数产生的误差比较大的,分裂这个组产生2个,这样加上开始那1个就有3个组了,然后再从这3个组里选一个分裂,产生4个组,重复此过程,产生5个组。这算是一中基本求精的思想。二分k均值不太受初始化的困扰,因为它执行了多次二分试验并选取具有最小误差的试验结果,还因为每步只有两个质心。
Kmeans++原理:
k-means++算法选择初始seeds的基本思想就是:初始的聚类中心之间的相互距离要尽可能的远。
- 从输入的数据点集合中随机选择一个点作为第一个聚类中心
- 对于数据集中的每一个点x,计算它与聚类中心(指已选择的聚类中心)的距离D(x),然后对于每一个点/总和得出一个概率,则第二个点依据概率进行选择。第三个点的选择是其他所有的点到前两个点的距离然后加和,再计算每一个点/总和的概率,再选择一个中心店。以此类推。。。。。
- 选择一个新的数据点作为新的聚类中心,选择的原则是:D(x)较大的点,被选取作为聚类中心的概率较大(概率化选择)
利用Canopy计算初始类簇中心点。
不需要迭代,比较快
步骤:
1.首先定义两个距离T1和T2,T1>T2.从初始的点的集合S中随机移除一个点P,然后对于还在S中的每个点I,计算该点I与点P的距离。
2.如果距离小于T1,则将点I加入到点P所代表的Canopy中,如果距离小于T2,则将点I从集合S中移除,并将点I加入到点P所代表的Canopy中。
3.迭代完一次之后,重新从集合S中随机选择一个点作为新的点P,然后重复执行以上步骤。
图示:
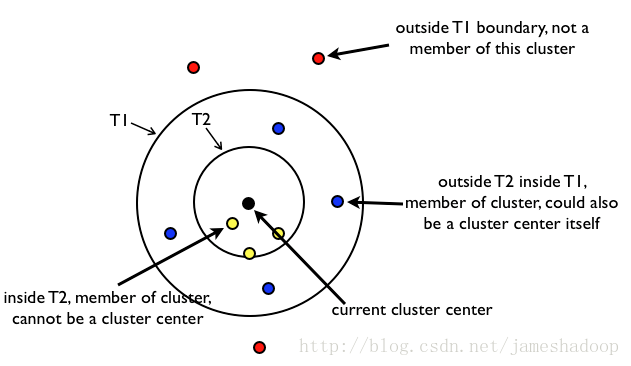
总结:与中心的距离大于T1时,这些点就不会被归入到中心所在的这个canopy类中。然当距离小于T1大于T2时,这些点会被归入到该中心所在的canopy中,但是它们并不会从D中被移除,也就是说,它们将会参与到下一轮的聚类过程中,成为新的canopy类的中心或者成员。亦即,两个Canopy类中有些成员是重叠的。而当距离小于T2的时候,这些点就会被归入到该中心的canopy类中,而且会从D中被移除,也就是不会参加下一次的聚类过程了。
三、代码
代码一:Kmeans实现
# !/usr/bin/python # -*- coding:utf-8 -*- import numpy as np import matplotlib.pyplot as plt import sklearn.datasets as ds import matplotlib.colors from sklearn.cluster import KMeans def expand(a, b): d = (b - a) * 0.1 return a-d, b+d if __name__ == "__main__": N = 400#400个数据点 centers = 4#4个中心店 data, y = ds.make_blobs(N, n_features=2, centers=centers, random_state=2)#聚类测试点 创建高沙分布的点 data2, y2 = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=(1, 2.5, 0.5, 2), random_state=2)#每个类别的标准差不一样,u是正态分布,胖瘦 data3 = np.vstack((data[y == 0][:], data[y == 1][:50], data[y == 2][:20], data[y == 3][:5]))#垂直放 每个类别生成一百个数据 每个类别拿的数据不一样。目的是每一个簇里面的密度不一样,看看聚类效果。 y3 = np.array([0] * 100 + [1] * 50 + [2] * 20 + [3] * 5)#自己构建label cls = KMeans(n_clusters=4, init='k-means++') y_hat = cls.fit_predict(data) y2_hat = cls.fit_predict(data2) y3_hat = cls.fit_predict(data3) m = np.array(((1, 1), (1, 3)))#矩阵点乘 ,相当于旋转 data_r = data.dot(m) y_r_hat = cls.fit_predict(data_r) matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] matplotlib.rcParams['axes.unicode_minus'] = False cm = matplotlib.colors.ListedColormap(list('rgbm')) plt.figure(figsize=(9, 10), facecolor='w') plt.subplot(421) plt.title(u'原始数据') plt.scatter(data[:, 0], data[:, 1], c=y, s=30, cmap=cm, edgecolors='none')#坐标轴 x1_min, x2_min = np.min(data, axis=0) x1_max, x2_max = np.max(data, axis=0) x1_min, x1_max = expand(x1_min, x1_max) x2_min, x2_max = expand(x2_min, x2_max) plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(422) plt.title(u'KMeans++聚类') plt.scatter(data[:, 0], data[:, 1], c=y_hat, s=30, cmap=cm, edgecolors='none') plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(423) plt.title(u'旋转后数据') plt.scatter(data_r[:, 0], data_r[:, 1], c=y, s=30, cmap=cm, edgecolors='none') x1_min, x2_min = np.min(data_r, axis=0) x1_max, x2_max = np.max(data_r, axis=0) x1_min, x1_max = expand(x1_min, x1_max) x2_min, x2_max = expand(x2_min, x2_max) plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(424) plt.title(u'旋转后KMeans++聚类') plt.scatter(data_r[:, 0], data_r[:, 1], c=y_r_hat, s=30, cmap=cm, edgecolors='none') plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(425) plt.title(u'方差不相等数据') plt.scatter(data2[:, 0], data2[:, 1], c=y2, s=30, cmap=cm, edgecolors='none') x1_min, x2_min = np.min(data2, axis=0) x1_max, x2_max = np.max(data2, axis=0) x1_min, x1_max = expand(x1_min, x1_max) x2_min, x2_max = expand(x2_min, x2_max) plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(426) plt.title(u'方差不相等KMeans++聚类') plt.scatter(data2[:, 0], data2[:, 1], c=y2_hat, s=30, cmap=cm, edgecolors='none') plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(427) plt.title(u'数量不相等数据') plt.scatter(data3[:, 0], data3[:, 1], s=30, c=y3, cmap=cm, edgecolors='none') x1_min, x2_min = np.min(data3, axis=0) x1_max, x2_max = np.max(data3, axis=0) x1_min, x1_max = expand(x1_min, x1_max) x2_min, x2_max = expand(x2_min, x2_max) plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.subplot(428) plt.title(u'数量不相等KMeans++聚类') plt.scatter(data3[:, 0], data3[:, 1], c=y3_hat, s=30, cmap=cm, edgecolors='none') plt.xlim((x1_min, x1_max)) plt.ylim((x2_min, x2_max)) plt.grid(True) plt.tight_layout(2, rect=(0, 0, 1, 0.97)) plt.suptitle(u'数据分布对KMeans聚类的影响', fontsize=18) # https://github.com/matplotlib/matplotlib/issues/829 # plt.subplots_adjust(top=0.92) # plt.show() plt.savefig('cluster_kmeans')
结果:
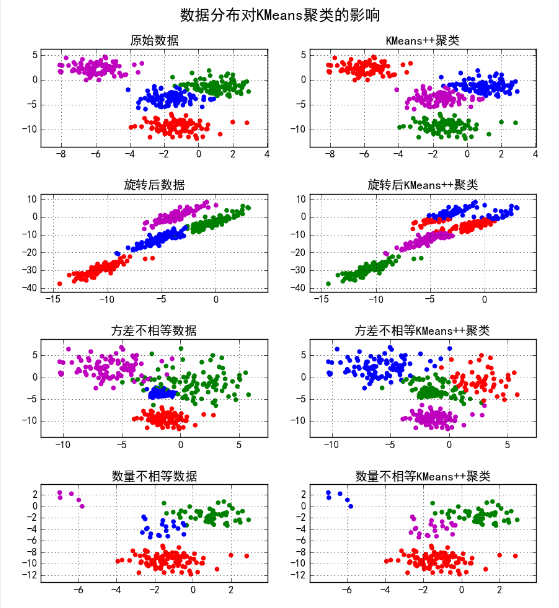
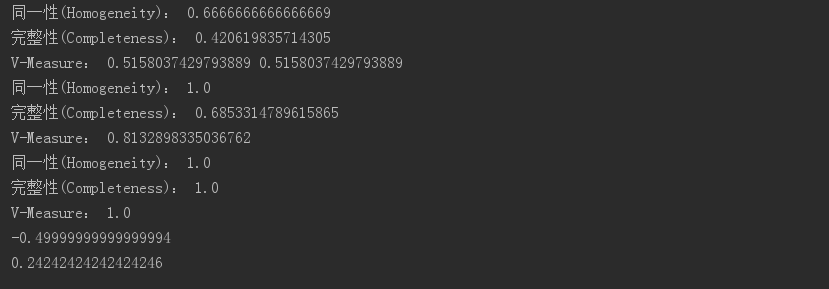
代码二:评估指标
# !/usr/bin/python # -*- coding:utf-8 -*- from sklearn import metrics#评估 if __name__ == "__main__": y = [0, 0, 0, 1, 1, 1] y_hat = [0, 0, 1, 1, 2, 2] h = metrics.homogeneity_score(y, y_hat) c = metrics.completeness_score(y, y_hat) print(u'同一性(Homogeneity):', h) print(u'完整性(Completeness):', c) v2 = 2 * c * h / (c + h) v = metrics.v_measure_score(y, y_hat) print(u'V-Measure:', v2, v) y = [0, 0, 0, 1, 1, 1] y_hat = [0, 0, 1, 3, 3, 3] h = metrics.homogeneity_score(y, y_hat) c = metrics.completeness_score(y, y_hat) v = metrics.v_measure_score(y, y_hat) print(u'同一性(Homogeneity):', h) print(u'完整性(Completeness):', c) print(u'V-Measure:', v) # 允许不同值 y = [0, 0, 0, 1, 1, 1] y_hat = [1, 1, 1, 0, 0, 0] h = metrics.homogeneity_score(y, y_hat) c = metrics.completeness_score(y, y_hat) v = metrics.v_measure_score(y, y_hat) print(u'同一性(Homogeneity):', h) print(u'完整性(Completeness):', c) print(u'V-Measure:', v) y = [0, 0, 1, 1] y_hat = [0, 1, 0, 1] ari = metrics.adjusted_rand_score(y, y_hat) print(ari) y = [0, 0, 0, 1, 1, 1] y_hat = [0, 0, 1, 1, 2, 2] ari = metrics.adjusted_rand_score(y, y_hat) print(ari)
均一性,一个簇中只包含一个类别样本,Precision
完整性,同类别样本被归到同一个簇中,Recall
V-Measure:
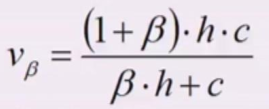




 浙公网安备 33010602011771号
浙公网安备 33010602011771号