PBR

PBR

微平面模型

       微表面模型是PBR中最重要的理论，几乎所有的PBR技术都基于微表面模型。理论认为任何平面都可以用细小镜面来描绘，只不过这些镜面的排布规则不一样，有的粗糙，有的光滑。这样就可以利用粗糙度这个参数对平面进行区分，或者是对一些性质进行计算。在光的反射中，越是光滑的表面其和法线相同的就越多。反射得到的光线也更加锐利，反之亦然。

 

能量守恒

       光线若要看起来更加真实，需要遵循能量守恒定理，当光线打入一个平面的时候，其大致被分为两部分，一部分是折射后进入平面内部转化为其他能量或经过分子间的数次反射后重新回到空间中的能量，另一部分是在表面直接被反射的能量。前一部分一般表现为漫反射，后一部分一般表现为镜面反射，更具有方向性。令这两部分能量守恒可以大致描绘能量守恒对光照表现的影响。一般做法是认为菲涅尔方程作为镜面反射的系数，这个系数描绘了光线在当前角度下直接弹回的比例，除此之外的另一部分认为是作为漫反射的能量。

辐射度量学

       辐射通量：描述的是一段时间内做的功。然后渲染中我们更关心某个时刻内光的特性，也就是功率。光的功率就是光通量，也就是单位时间内通过某个区域的总能量。可以通过对能量进行时间的微分来获取光通量;

流明 lumen：辐射通量相同的两个光源，如果发射的是不同波长的光波，对人眼睛所能引起的亮暗度感觉也不一样，也就是说他们有不同的发光效率，发光效率越高，人眼也会觉的越亮。因此真正影响人眼视觉明暗感受的是辐射通量于发光效率的乘积，也就是我们所说的光通量，单位是流明（lm）；

Radiant Intensity：Radiant Intensity是点光源发出的每单位立体角的能量 ；

Irradiance：是入射在表面点上的每单位面积的能量（光线和单位面积不垂直要投影到垂直的方向上去）随着球壳的增大，光的强度会有一个距离平方的衰减，这里的衰减其实也是Irradiance在衰减

Radiance：是为了用来描述环境中光线在空间中传播的一些属性，是每单位立体角，每单位投影面积发射、反射、发射或接收的能量；

 

BRDF

       BRDF也叫双向反射分布函数，他的输入参数为入射光的方向、出射光的方向、平面发现、以及一个粗糙度。通过对这几个参数的处理近似求出每一束光线在当前状态下对最终物体表面反射出来的光线的贡献程度。Blinn-Phone可以认为是一种没有遵循能量守恒BRDF。BRDF反应的是直接光照在PBS中的作用。

Cook-Torrance反射率方程

      

 

 

       其中Kd和Ks分别是能量比例系数，用来Kd+Ks=1。前半部分表示的是漫反射，后半部分表示的是镜面反射。

其中漫反射部分可以表示为：

 

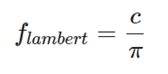
       而镜面反射部分则相对负责，可以大致分为三个函数：法线分布函数，菲涅尔方程和几何函数。发现分布函数表示在粗糙度的影响，去向方向与中间向量一致的微平面的数量。这是用来估算微平面的主要函数。几何函数描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候，平面表面上的微平面可能挡住其他的微平面从而减少表面所反射的光线。菲涅尔方程描述的是在不同的表面角下表面所反射的光线所占的比率。

 

法线分布函数

       发现分布函数也是镜面分布，即在当前入射角度下。打到微平面上后反射的光线朝向和反射向量一致的光线的比例。公式可以表示为：

 

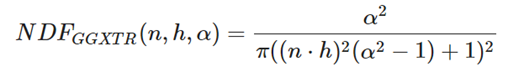
       几何函数

       由于微表面是粗糙不平的，因此几何函数提供的是在一定入射角度和粗糙度的情况下被微表面遮挡的光线比例，这里面分为入射时被遮挡和出射时被遮挡的比例。单向遮蔽的公式如下：

 

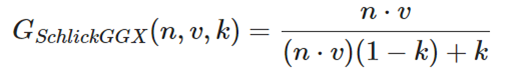
       这表示的只是单项遮蔽，但是遮蔽分为入射和出射两部分。一次最终的结果是将两个方向相乘的。

 

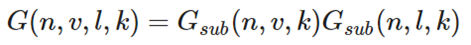
       菲涅尔方程

       方程描述的是被反射的光线对比光线被折射的部分所占的比率，这个比率会随着我们观察的角度不同而不同。当光线碰撞到一个表面的时候，菲涅尔方程会根据观察角度告诉我们被反射的光线所占的百分比。利用这个反射比率和能量守恒原则，我们可以直接得出光线被折射的部分以及光线剩余的能量。可以用公式表示如下：

 

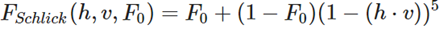
蒙特卡洛积分

       蒙特卡罗积分建立在大数定律的基础上，并采用相同的方法来求解积分。不为所有可能的（理论上是无限的）样本值 x 求解积分，而是简单地从总体中随机挑选样本 N 生成采样值并求平均。随着 N的增加，我们的结果会越来越接近积分的精确结果：

 

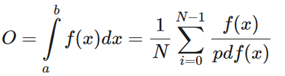
       实际上这也是一个离散化的过程，用大量的离散化样本来拟合真正的积分结果。为了使收敛更快，往往采用一个叫低差异序列的东西，它可以把无规则的随机样本变得更加平均。

       然而在实际中，反射光线往往集中在一个叶状的波瓣内，因此，在得出采样样本的时候可以对随机生成的采样向量转换到这个波瓣内，这被称为重要性采样（GGX）。

基于环境的光照 IBL

       现实中的环境光照实际上是来自与环境中的各种间接光照，然而有间接光照就有反射的物体，因此基于环境的光照就离不开从环境中采样光照。这里考虑对天空盒进行光照采样。

首先反射方程可以表示为：

 

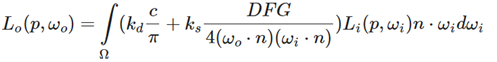
这个公式的前半部分是漫反射，后半部分是镜面反射，因此就可以把这个公式拆成两半。

 

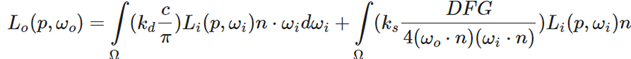
       最后将两部分分别求积分。

       漫反射辐照IBL

       先看公式的前半部分：

 

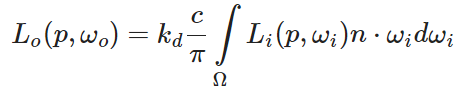
       由于漫反射辐照在计算片段的时候不考虑方向，可以求积分同样可以采用求利曼和的形式求积分，实际上也是一种离散化的方法，目前没有特别好的解析法求解积分的方式。这种方式能较好地逼近真是结果。将积分公式离散化可以得到以下公式：

 

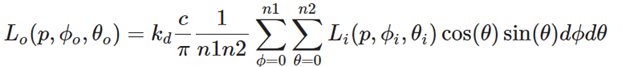
       转换为离散公式后就可以将采样区域分片后求平均了。这其中第二个参数代表分片中的横坐标，第三个代表纵坐标，即仰角。cos可以表达不同角度下光线的贡献，而sin可以表达随着仰角的升高导致的采样片段面积缩小的因素。

       最后还要考虑一个问题，如果在每一帧中都这样进行采样，那代价就太昂贵了。由于环境光照可以不考虑方向只考虑能量，因此可以对环境进行预处理。可以通过对环境光照贴图求卷积的形式进行预处理，在使用的时候只需要根据当前渲染片段的法线指向的卷积贴图部分进行采样即可。采样的预处理贴图的采样位置的结果即为卷积结果。卷积实际上也是对一定范围内值的平均。

       镜面IBL

       镜面IBL即基于物理的环境光照的镜面反射部分。

 

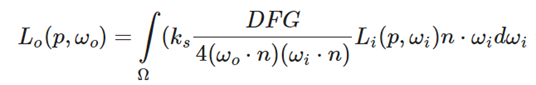
       这部分公式涉及的输入变量过多，无法在合理的时间复杂度内进行预计算。因此需要对公式进行拆分，最后求一个叫做slite sum的公式，该公式将上面的公式一分为二，但不是完全相等的关系，只是对上式的一个近似。

 

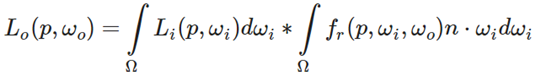
       这样就可以对公式进行分开求值后再求积就行了。

       先看前半部分。前半部分由于剥离了观察角度，但计算辐照的时候需要考虑角度，就可以把观察角度和反射角度都默认为和法线一致。根据粗糙度不同反射波瓣也是不同的，但是波瓣的方向对范围的影响可以暂且不考虑。因此就可以采用这种近似的方法。在后面根据反射方向进行采样的时候的偏差不会太大，算是一种妥协。用重要性采样将随机采样向量映射到波瓣范围内求蒙特卡洛积分即可预处理出来一个卷积贴图，这个贴图表示的是当前采样位置的辐照度。别称为：预滤波环境光贴图用作采样。

       再看后半部分。后半部分主要就是根据观察方向、粗糙度、初始反射率。但是由于初始反射率是一个三维向量，因此需要把他提出来，对公式做如下变形：

 

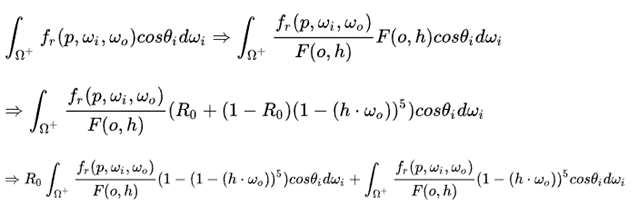
       这样就又可以将式子划分为两部分，求出结果后预存在一个贴图中使用时查询即可。这个贴图成为LUT。

       被分出来的两部分可以表示为：

 

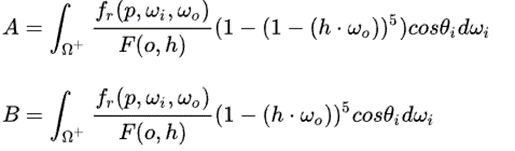
       这样就可以按照和之前类似的方法进行分别离散计算，将结果存在一张贴图中的R通道和G通道中即可用作查询。二维贴图可以用夹角和粗糙度进行查询反应结果。最后将以上结果组合起来就得到了IBL的结果。

 

参考资料

https://zhuanlan.zhihu.com/p/473902856

https://www.cnblogs.com/herenzhiming/articles/5789043.html

https://zhuanlan.zhihu.com/p/21376124

https://zhuanlan.zhihu.com/p/37639418

https://learnopengl.com/PBR/Theory

https://www.cnblogs.com/timlly/p/10631718.html

https://zhuanlan.zhihu.com/p/370207345