P3242 [HNOI2015] 接水果

P3242 [HNOI2015] 接水果

题目描述

风见幽香非常喜欢玩一个叫做 osu! 的游戏，其中她最喜欢玩的模式就是接水果。由于她已经 DT FC 了 The big black，她觉得这个游戏太简单了，于是发明了一个更加难的版本。

首先有一个地图，是一棵由 \(n\) 个顶点，\(n-1\) 条边组成的树。

这颗树上有 \(p\) 个盘子，每个盘子实际上是一条路径，并且每个盘子还有一个权值。第 \(i\) 个盘子就是顶点 \(a_i\) 到顶点 \(b_i\) 的路径（由于是树，所以从 \(a_i\) 到 \(b_i\) 的路径是唯一的），权值为 \(c_i\)。

接下来依次会有 \(q\) 个水果掉下来，每个水果本质上也是一条路径，第 \(i\) 个水果是从顶点 \(u_i\) 到顶点 \(v_i\) 的路径。

幽香每次需要选择一个盘子去接当前的水果：一个盘子能接住一个水果，当且仅当盘子的路径是水果的路径的子路径。这里规定：从 \(a\) 到 \(b\) 的路径与从 \(b\) 到 \(a\) 的路径是同一条路径。

当然为了提高难度，对于第 \(i\) 个水果，你需要选择能接住它的所有盘子中，权值第 \(k_i\) 小的那个盘子，每个盘子可重复使用（没有使用次数的上限：一个盘子接完一个水果后，后面还可继续接其他水果，只要它是水果路径的子路径）。幽香认为这个游戏很难，你能轻松解决给她看吗？

输入格式

第一行三个数 \(n\) 和 \(p\) 和 \(q\)，表示树的大小和盘子的个数和水果的个数。

接下来 \(n-1\) 行，每行两个数 \(a,b\)，表示树上的 \(a\) 和 \(b\) 之间有一条边。树中顶点按 \(1\) 到 \(n\) 标号。

接下来 \(p\) 行，每行三个数 \(a,b,c\)，表示路径为 \(a\) 到 \(b\)、权值为 \(c\) 的盘子，其中 \(a \neq b\)。

接下来 \(q\) 行，每行三个数 \(u,v,k\)，表示路径为 \(u\) 到 \(v\) 的水果，其中 \(u \neq v\)，你需要选择第 \(k\) 小的盘子，第 \(k\) 小一定存在。

输出格式

对于每个果子，输出一行表示选择的盘子的权值。

数据范围

对于 \(100\%\) 的数据，\(1\leq n,p,q \leq4\times 10^4\)，\(0 \le c \le 10^9\)。

Solution:

整体二分好题。

整体二分：

参考我们之前学过的二分答案这一思想，整体二分的还是而分一个答案，然后统计一下对于当前答案 \(ans\) 是那些询问的答案。由于我们处理每个叶子 \(ans\) 时，必定会有一个及以上的询问和他对应，所以复杂度不会太高，是 \(O(mlogV)\) 的。

问题转化:

首先分析一下这个反常识的题面，我们要用水果去接盘子。

如果盘子的路径是一条链：

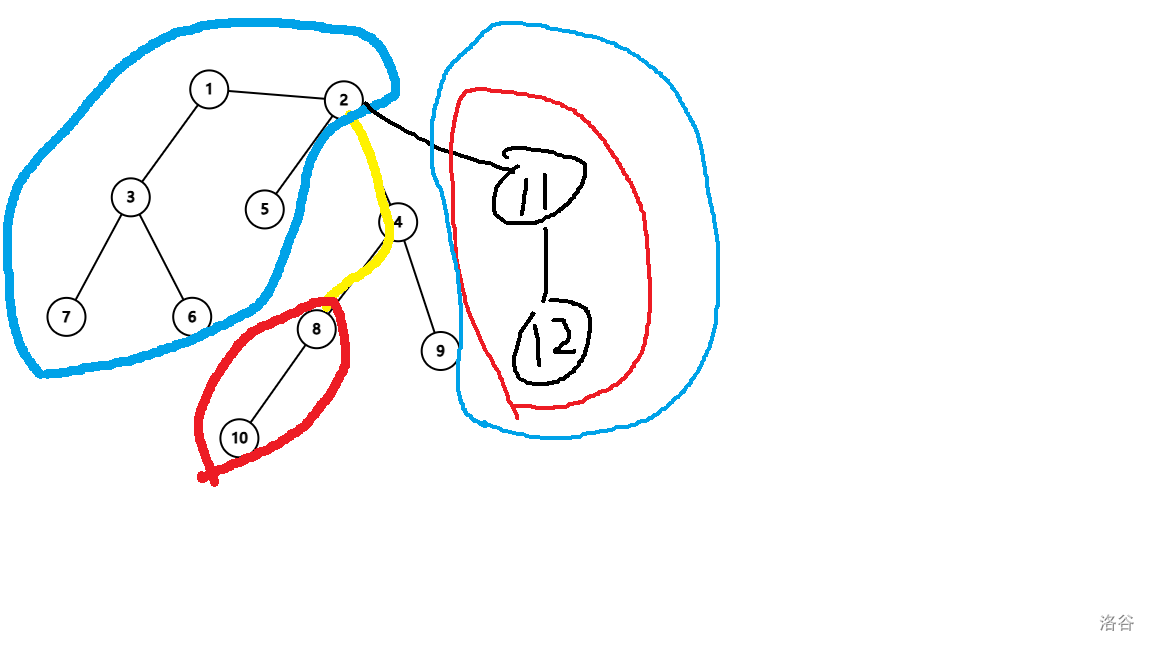
我们会发现 (2,8) 这条路径会对起点在篮圈，终点在红圈内的点产生贡献。

我们假设盘子的起终点是 \((x,y)\) , \(dep_x<dep_y\) 设 \(z\) 是从 \(z\) 出发，路径 \((x,y)\) 的起始边的终点 (图中是 4)。

那么我们就可以用 \([1,st_z) \cup [st_y,ed_y)\) 来刻画起点，那么这两个起点集 分别 对应的终点集就是 \([st_y,ed_y],(ed_z,n]\)

再来看不在一条链上：

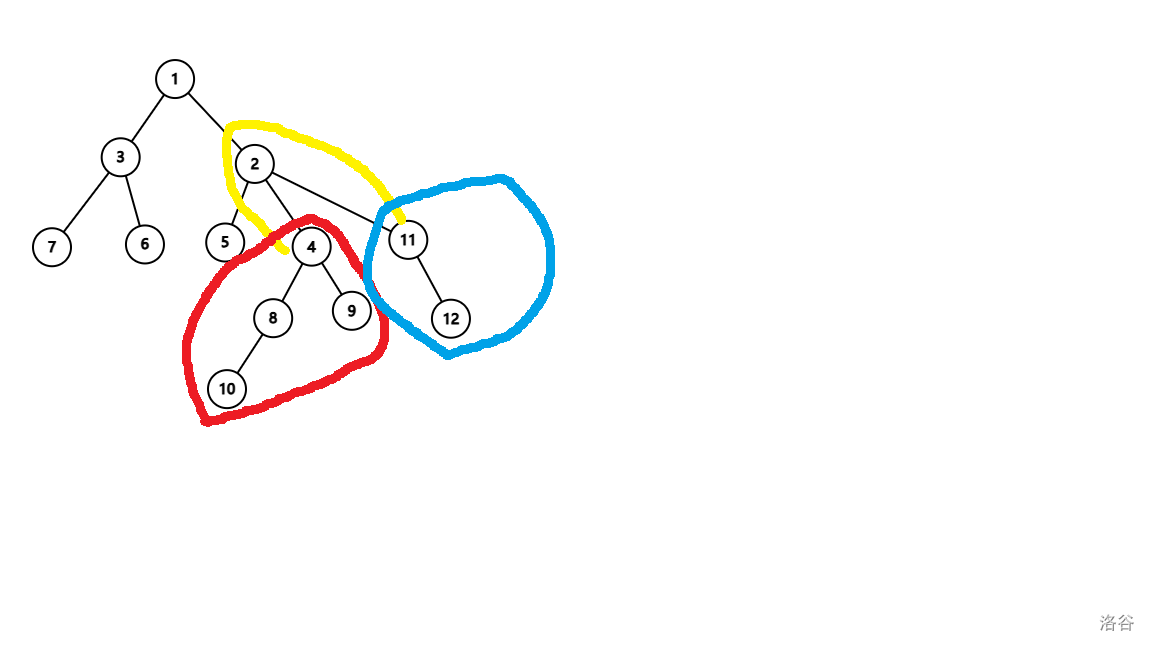
很显然路径 (x,y) 会对起点在 \([st_x,ed_x]\) 且终点在 \([st_y,ed_y]\) 的水果有贡献。

现在我们将起点看成 x轴，终点看成 y轴。那么我们的每个盘子就相当于给几个矩形插入了一个新的值，那么查询就是要查一个单点上的所有将其包含的矩形中，权值第 \(k\) 的小的矩形。

这是一个经典的扫描线，我们以后用树状数组实现一个前缀和，然后将矩形变为在前缀和数组上差分。

算法实现：

我们先将所有的区间修改和单点查询按照 \(x\) 坐标排个序，我们先加入后查询。

我们需要实现一个 solve(L,R,l,R) 函数。表示只考虑权值在 \([l,r]\) 内的矩形，对于标号在 \([L,R]\) 内的操作进行答案统计。

然后我们考虑如何分治：

先说修改：
由于我们的修改是在前缀和数组上差分的，所以只要一条线的权值 \(val\) 满足 \(mid<=val\) 那么就将其加入树状数组中，然后将其划分到右区间内，反之不修改，直接划分到左区间。

我们记 \(tmp\) 表示只考虑权值在 \([l,mid]\) 内的矩形时，\((x,y)\) 这个位置被 \(tmp\) 个矩形覆盖。
如果 \(tmp<k\) 则说明 \([l,mid]\) 内没有这个询问的答案，我们将这个询问划分到右区间，反之划分到左区间。

当一个 solve 函数运行到叶子 \(l=r\) 时，当前节点上挂的所有询问的答案都是 \(l\) 。所以我们只会分 \(logV\) 层，每层处理的任务个数都是 \(O(n)\) 级别的，然后树状数组的复杂度是 \(logn\) 所以总复杂度不会太高。

Code:

#include<bits/stdc++.h>
const int N=4e4+5;
const int lg=17;
using namespace std;
int n,m,p,tot,cnt;
int t[N],dep[N],st[N],ed[N];
int f[N][lg+1],val[N],ans[N];
vector<int> E[N];
struct task{
    int opt,x,l,r,k,v,id;
    bool operator <(const task &a)const{
        return x==a.x ? opt < a.opt : x<a.x;
    }
}q[N*5],ql[N*5],qr[N*5];
inline int lowbit(int x){return x&-x;}
inline void upd(int x,int k)
{
    for(;x<=n;x+=lowbit(x))t[x]+=k;
}
inline int sum(int x)
{
    int res=0;
    for(;x;x-=lowbit(x))res+=t[x];
    return res;
}
void dfs(int x,int fa)
{
    dep[x]=dep[f[x][0]=fa]+1;st[x]=++tot;
    for(int j=1;j<=lg;j++)f[x][j]=f[f[x][j-1]][j-1];
    for(int y : E[x])if(y!=fa)dfs(y,x);ed[x]=tot;
}
int LCA(int x,int y)
{
    if(dep[x]<dep[y])swap(x,y);
    for(int i=lg;i>=0;i--)if(dep[f[x][i]]>=dep[y])x=f[x][i];
    for(int i=lg;i>=0;i--)if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];
    return x==y ? x : f[x][0];
}
int find(int x,int y)
{
    for(auto z : E[x])if(z!=f[x][0]&&st[z]<=st[y]&&st[y]<=ed[z])return z;
}
void solve(int L,int R,int l,int r)//id:[L,R] val:[l,r]
{
    if(L>R)return;
    //cout<<L<<" "<<R<<":"<<l<<" "<<r<<"\n";
    if(l==r){for(int i=L;i<=R;i++)ans[q[i].id]=val[l];return;}
    int mid=l+r>>1,tmp,cntl=0,cntr=0;
    for(int i=L;i<=R;i++)
    {
        if(q[i].opt==1)
        {
            if(q[i].k<=mid)
            {
                upd(q[i].l,q[i].v);upd(q[i].r+1,-q[i].v);
                ql[++cntl]=q[i];
            }else qr[++cntr]=q[i];
        }
        else
        {
            tmp=sum(q[i].l);
            if(q[i].k<=tmp)ql[++cntl]=q[i];
            else q[i].k-=tmp,qr[++cntr]=q[i];
        }
    }
    tmp=L-1;
    for(int i=1;i<=cntl;i++)q[++tmp]=ql[i];
    for(int i=1;i<=cntr;i++)q[++tmp]=qr[i];
    solve(L,L+cntl-1,l,mid);solve(L+cntl,R,mid+1,r);
}
void work()
{
    cin>>n>>m>>p;
    for(int i=1,x,y;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        E[x].emplace_back(y);
        E[y].emplace_back(x);
    }
    for(int u=1;u<=n;u++)reverse(E[u].begin(),E[u].end());
    dfs(1,0);
    for(int i=1,x,y,k,z;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&k);val[i]=k;
        if(st[x]>st[y])swap(x,y);int lca=LCA(x,y);
        if(x==lca)
        {
            z=find(x,y);
            if(1<st[z])
            {
                q[++cnt]={1,1,st[y],ed[y],k,1,0};
                q[++cnt]={1,st[z],st[y],ed[y],k,-1,0};
            }
            if(ed[z]<n)
            {
                q[++cnt]={1,st[y],ed[z]+1,n,k,1,0};
                q[++cnt]={1,ed[y]+1,ed[z]+1,n,k,-1,0};
            }
        }
        else
        {
            q[++cnt]={1,st[x],st[y],ed[y],k,1,0};
            q[++cnt]={1,ed[x]+1,st[y],ed[y],k,-1,0};
        }
    }
    sort(val+1,val+1+m);
    int inf=unique(val+1,val+1+m)-val-1;
    for(int i=1;i<=cnt;i++)q[i].k=lower_bound(val+1,val+1+inf,q[i].k)-val;
    for(int i=1,x,y,k;i<=p;i++)
    {
        scanf("%d%d%d",&x,&y,&k);
        if(st[x]>st[y])swap(x,y);
        q[++cnt]={2,st[x],st[y],0,k,0,i};
    }
    sort(q+1,q+1+cnt);
    solve(1,cnt,1,inf);
    for(int i=1;i<=p;i++)
    {
        printf("%d\n",ans[i]);
    }
}
int main()
{
    work();
    return 0;
}