P2934 [USACO09JAN] Safe Travel G
P2934 [USACO09JAN] Safe Travel G
【题目描述】
给定一张有 \(n\) 个节点,\(m\) 条边的无向图,对于任意的 \(i\)(\(2\le i\le n\)),请求出在不经过原来 \(1\) 节点到 \(i\) 节点最短路上最后一条边的前提下,\(1\) 节点到 \(i\) 节点的最短路。
特别地,保证 \(1\) 到任何一个点 \(i\) 的最短路都是唯一的。
保证图中没有重边和自环。
数据范围:
\[N \le 10^5,M\le 2*10^5
\]
solution:
十分趣味的最短路+并查集
首先我们求一遍单源最短路并求出最短路树,然后考虑如何刻画本题的限制
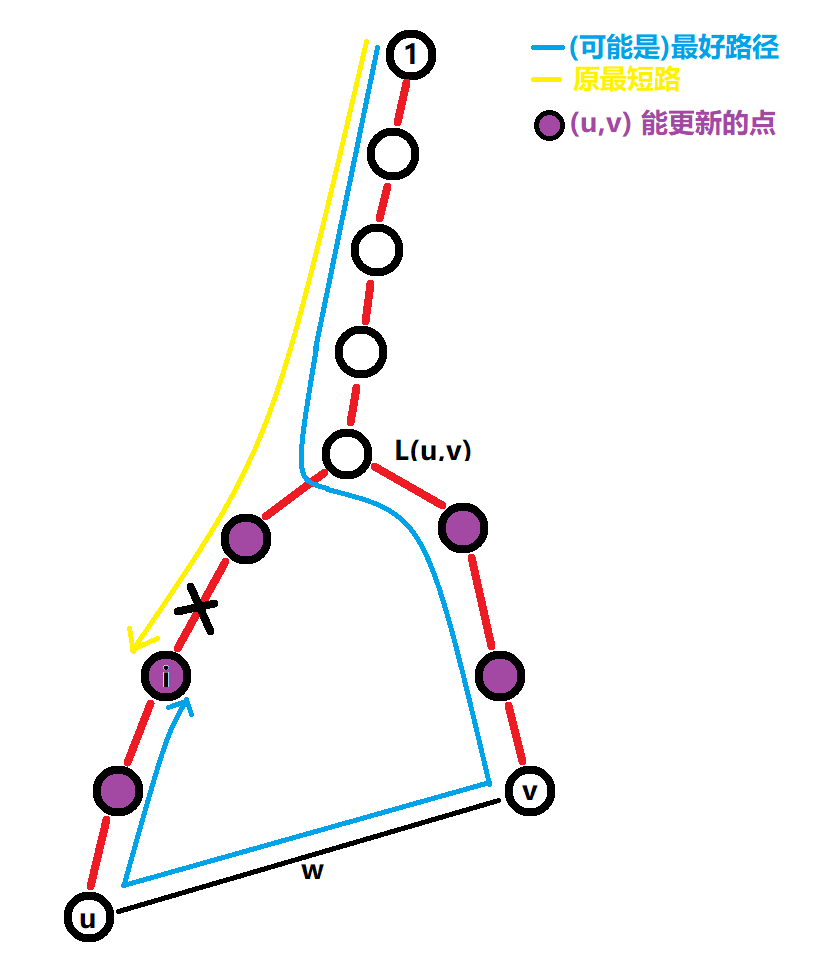
我们发现,对于一条非树边 (u,v) 他可能对在 (u->v) 路径上的点 \(i\) 产生贡献:
\[ans_{i}=min(ans_{i},dis_{u}+dis_{v}+w-dis_{i})
\]
然后我们发现 \(dis_{u}+dis_{v}+w\) 只和边本身有关.所以我们考虑将所有非树边按照 \(dis_{u}+dis_{v}+w\) 排序,然后对于一个点 \(i\) 其实它只会被更新一次(因为排过序了).而且我们也并不想要遍历整个路径带来的巨大时间复杂度,所以我们在对一个点 \(i\) 统计过答案过后,就将其缩到其父亲上,用并查集维护,然后这题就做完了
Code:
#include<bits/stdc++.h>
const int lg=20;
const int N=2e5+5;
const int inf=1e9;
using namespace std;
struct Node{
int id,val;
bool operator <(const Node &e)const{
return e.val<val;
}
};
int dis[N],vis[N],fa[N],ans[N],dep[N];
int f[N][lg+5];
priority_queue<Node> Q;
void init()
{
for(int i=0;i<N;i++)dis[i]=inf;
}
struct Edge{
int y,w,nxt;
}e[N<<1];
int head[N];
void add(int x,int y,int w)
{
e[++head[0]]={y,w,head[x]};
head[x]=head[0];
}
void dijkstra(int s)
{
init();
dis[s]=0;
Q.push({s,dis[s]});
while(!Q.empty())
{
int u=Q.top().id;Q.pop();
if(vis[u])continue;
vis[u]=1;
for(int i=head[u],v,w;i;i=e[i].nxt)
{
v=e[i].y,w=e[i].w;
if(dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
f[v][0]=u;dep[v]=dep[u]+1;
Q.push({v,dis[v]});
}
}
}
}
struct EDge{
int x,y,val;
bool operator <(const EDge &e)const{
return val<e.val;
}
}E[N];
int n,m,cnt;
int find(int x){return fa[x]= fa[x]==x ? fa[x] : find(fa[x]);}
void work()
{
cin>>n>>m;
for(int i=1,x,y,w;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&w);
add(x,y,w);
add(y,x,w);
}
dijkstra(1);
for(int u=1;u<=n;u++)
{
fa[u]=u;ans[u]=-1;
for(int i=head[u],v,w;i;i=e[i].nxt)
{
v=e[i].y,w=e[i].w;
if(f[u][0]!=v&&f[v][0]!=u&&u<v)
{
E[++cnt]={u,v,dis[u]+dis[v]+w};
}
}
}
sort(E+1,E+1+cnt);
for(int i=1;i<=cnt;i++)
{
int u=E[i].x,v=E[i].y,val=E[i].val;
int x=find(u),y=find(v);
while(x!=y)
{
if(dep[x]<dep[y])swap(x,y);
ans[x]=val-dis[x];
fa[x]=f[x][0];x=find(x);
}
}
for(int i=2;i<=n;i++)
{
printf("%d\n",ans[i]);
}
}
int main()
{
//freopen("P2934_2.in","r",stdin);freopen("travel.out","w",stdout);
work();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号