P2537 [AHOI2005] 穿越磁场
P2537 [AHOI2005] 穿越磁场
好久以前就加了题单的好题
可你就是不写是吧(/‵Д′)/~ ╧╧
题目描述
探险机器人在Samuel星球上寻找一块奇特的矿石,然而此时它陷入了一片神秘的磁场区域,动弹不得。
探险空间站立刻扫描了这片区域,绘制出该区域的磁场分布平面图。这片区域中分布了N个磁场,每个磁场呈正方形,且边与坐标轴平行。
例如下图中,存在3个磁场,白点表示机器人的位置,黑点表示矿石的位置:
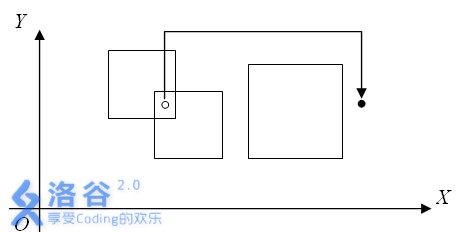
科学家们分析平面图,进一步发现:这些磁场为大小不一的正方形,可能相交,甚至覆盖,但是它们的边缘不会重合,顶点也不会重合。
例如下面的两种情形是不会出现的:
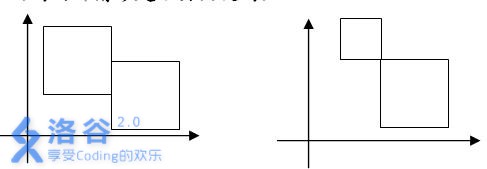
科学家们给探险机器人启动了磁力罩,这样它就可以在磁场中自由穿越了。
初始时,探险机器人和所有矿石都不在任何磁场的边缘。由于技术限制,在穿越过程中机器人只能够水平或垂直移动,且不能够沿着磁场的边缘行动。
由于磁力罩的能量有限,科学家们希望探险机器人穿越尽量少的磁场边缘采集到这块矿石。例如上图中,探险机器人最少需要穿越两次磁场边缘。
现在小联请你编写程序,帮助科学家们设计探险机器人的路线,统计探险机器人最少需要穿越多少次磁场边缘。
Solution:
只要我们发现虽然坐标很大,但是n并不大,所以我们可以将
但是要注意的是,由于本题建图比较抽象,所以在连边时一点要细心且思路明确
Link:
for(int i=1;i<=n;i++) { int x1=q[i].x1,y1=q[i].y1,x2=q[i].x2,y2=q[i].y2; // 0:up 1:down 2:left 3:right for(int xx=x1;xx<x2;xx++){w[xx][y1-1][3]=w[xx][y1][2]=w[xx][y2-1][3]=w[xx][y2][2]=1;} for(int yy=y1;yy<y2;yy++){w[x2-1][yy][1]=w[x2][yy][0]=w[x1][yy][0]=w[x1-1][yy][1]=1;} }
Code:
#include<bits/stdc++.h> const int N=105; const int M=105*105*2; const int inf=1e9; using namespace std; int x[M],y[M]; int dx[4]={-1,1,0,0}; int dy[4]={0,0,-1,1}; int w[N<<1][N<<1][4]; struct square{ int x1,y1,x2,y2; }q[N]; int n,sx,sy,ex,ey; int dis[N<<1][N<<1],vis[N<<1][N<<1]; void init() { for(int i=1;i<x[0];i++)for(int j=1;j<y[0];j++)dis[i][j]=inf; } struct Node{ int x,y,val; bool operator <(const Node &e)const{ return e.val<val; } }; priority_queue<Node> Q; void dijkstra() { init(); dis[sx][sy]=0; Q.push(Node{sx,sy,0}); while(!Q.empty()) { Node u=Q.top();Q.pop(); if(u.x==ex&&u.y==ey)return; if(vis[u.x][u.y])continue; vis[u.x][u.y]=1; for(int i=0;i<4;i++) { int xx=u.x+dx[i],yy=u.y+dy[i]; if(xx<1||x[0]<=xx)continue; if(yy<1||y[0]<=yy)continue; if(dis[xx][yy]>dis[u.x][u.y]+w[u.x][u.y][i]) { dis[xx][yy]=dis[u.x][u.y]+w[u.x][u.y][i]; Q.push(Node{xx,yy,dis[xx][yy]}); } } } } void work() { cin>>n; for(int i=1,xx,yy,dd;i<=n;i++) { scanf("%d%d%d",&xx,&yy,&dd); x[++x[0]]=xx,x[++x[0]]=xx+dd; y[++y[0]]=yy,y[++y[0]]=yy+dd; q[i]={xx,yy,xx+dd,yy+dd}; } x[++x[0]]=inf,x[++x[0]]=-inf; y[++y[0]]=inf,y[++y[0]]=-inf; sort(x+1,x+1+x[0]);sort(y+1,y+1+y[0]); x[0]=unique(x+1,x+1+x[0])-(x+1); y[0]=unique(y+1,y+1+y[0])-(y+1); for(int i=1;i<=n;i++) { q[i]={ lower_bound(x+1,x+1+x[0],q[i].x1)-(x+1)+1, lower_bound(y+1,y+1+y[0],q[i].y1)-(y+1)+1, lower_bound(x+1,x+1+x[0],q[i].x2)-(x+1)+1, lower_bound(y+1,y+1+y[0],q[i].y2)-(y+1)+1 }; } for(int i=1;i<=n;i++) { int x1=q[i].x1,y1=q[i].y1,x2=q[i].x2,y2=q[i].y2; // 0:up 1:down 2:left 3:right for(int xx=x1;xx<x2;xx++){w[xx][y1-1][3]=w[xx][y1][2]=w[xx][y2-1][3]=w[xx][y2][2]=1;} for(int yy=y1;yy<y2;yy++){w[x2-1][yy][1]=w[x2][yy][0]=w[x1][yy][0]=w[x1-1][yy][1]=1;} } cin>>sx>>sy>>ex>>ey; sx=lower_bound(x+1,x+1+x[0],sx)-x;ex=lower_bound(x+1,x+1+x[0],ex)-x; sy=lower_bound(y+1,y+1+y[0],sy)-y;ey=lower_bound(y+1,y+1+y[0],ey)-y; sx--,sy--,ex--,ey--; dijkstra(); printf("%d\n",dis[ex][ey]); } int main() { //freopen("P2537.in","r",stdin);freopen("P2537.out","w",stdout); work(); return 0; }



