P7834 [ONTAK2010] Peaks 加强版

P7834 [ONTAK2010] Peaks 加强版

[ONTAK2010] Peaks 加强版

题目背景

原题链接：P4197 Peaks

题目描述

给定一张 \(n\) 个点、\(m\) 条边的无向图，第 \(i\) 个点的权值为 \(a_i\)，边有边权。

有 \(q\) 组询问，每组询问给定三个整数 \(u, x, k\)，求从 \(u\) 开始只经过权值 \(\leq x\) 的边所能到达的权值第 \(k\) 大的点的权值，如果不存在输出 \(-1\)。

本题强制在线。

对于 \(100\%\) 的数据，\(1 \leq n \leq 10^5\)，\(0 \leq m, q \leq 5 \times 10^5\)。

说句闲话

感谢著名未来416之光 @XiaoZi_qwq 的推荐

Solution:

一个很新的东西：kruskal重构树

大概意思就是说，在 kruskal 时，对于两个应该连边的点 \((u,v,w)\) ，别急着连边，新建一个点 \(x\) 点权为 \(w\) 然后连两条边：\(x->u,x->v\) 这样建出来的一棵树上，所有叶子节点都由实点构成，两个实点的 \(lca\) 的点权就是二者的边权

图的话就借用一下 @asd369 大佬的：

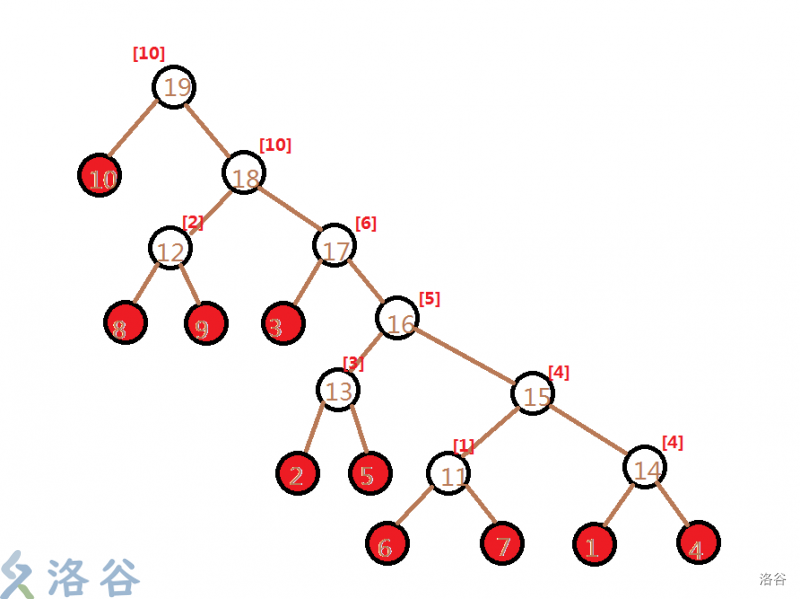
如图，这是一个最小生成树的 kruskal 重构树，它是一个大根堆。

有了这个东西之后这题就好做了：

首先，我们建出 kruskal 重构树，然后对它求欧拉序。对于每个询问 \((u,x,k)\) 我们从 \(u\) 开始向上倍增直到一个点 \(v\) 的点权严格大于 \(x\) 然后我们再在以 \(v\) 为根的子树下求第 \(k\) 大值就好了

而求第 \(k\) 大这显然是主席树的活

需要注意的是我们的主席树是根据欧拉序的第一次访问来顺序建的，只有这样才能满足先祖关系

警钟长鸣:

注意数据范围以及值域

Code:

#include<bits/stdc++.h>
const int N=2e5+5;
const int inf=1e9;
const int lg=25;
using namespace std;
int e_cnt,n,m,q,ans;
int a[N],b[N],w[N<<1];
int head[N<<1];
struct Edge{
    int to,nxt;
}e[N<<2];
void add(int x,int y)
{
    e[++e_cnt]={y,head[x]};
    head[x]=e_cnt;
}
struct Kruskal{
    int tot;
    struct edge{
        int u,v,w;
        bool operator <(const edge &e)const{
            return w<e.w;
        }
    }q[N*5];
    int fa[N<<1];
    int find(int x){return fa[x] = fa[x]==x ? fa[x] : find(fa[x]);}
    void build()
    {
        tot=n;
        for(int i=1;i<=n<<1;i++)fa[i]=i;
        for(int i=1;i<=m;i++)scanf("%d%d%d",&q[i].u,&q[i].v,&q[i].w);
        sort(q+1,q+1+m);
        for(int i=1;i<=m;i++)
        {
            int x=find(q[i].u),y=find(q[i].v);
            if(x!=y)
            {
                w[++tot]=q[i].w;
                add(tot,x);add(tot,y);
                fa[tot]=fa[x]=fa[y]=tot;
            }
        }
    }

}K;
struct Grapth{
    int tot=0;
    int f[N<<1][lg+5];
    int siz[N<<1],st[N<<1],ed[N<<1],rid[N<<1];
    void dfs(int x,int fa)
    {
        f[x][0]=fa;
        rid[++tot]=x;st[x]=tot;
        for(int j=1;j<=lg;j++)
        {
            f[x][j]=f[f[x][j-1]][j-1];
        }
        for(int i=head[x];i;i=e[i].nxt)
        {
            int y=e[i].to;
            if(y==f[x][0])continue;
            dfs(y,x);
            siz[x]+=siz[y];
        }
        if(!siz[x])siz[x]=1;
        ed[x]=tot;
    }
}G;
//Segment_Tree
struct Segment_Tree{
    int rt[N<<1];
    int cnt;
    struct Tree{
        int ls,rs,cnt;
    }t[N*80];
    void insert(int &x,int y,int l,int r,int k)
    {
        t[x=++cnt]=t[y];
        t[x].cnt++;
        if(l==r)return;
        int mid=l+r>>1;
        if(k<=mid)insert(t[x].ls,t[y].ls,l,mid,k);
        if(mid<k)insert(t[x].rs,t[y].rs,mid+1,r,k);
    }
    int query(int x,int y,int l,int r,int k)
    {
        if(l==r)return l;
        int Cnt=-t[t[x].rs].cnt+t[t[y].rs].cnt;
        int mid=l+r>>1;
        if(k<=Cnt) return query(t[x].rs,t[y].rs,mid+1,r,k);
        else return query(t[x].ls,t[y].ls,l,mid,k-Cnt);
    }
}T;
void change(int &x)
{
    x=(x^ans)%n + 1;
}
void work()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);b[i]=a[i];
    }
    //sort(b+1,b+1+n);
    //for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+1+n,a[i])-b;
    K.build();
    for(int i=K.tot;i;i--)
    {
        if(!G.siz[i])
        G.dfs(i,0);
    }
    for(int i=1;i<=K.tot;i++)
    {
        int x=G.rid[i];
        if(x<=n)
        {
            T.insert(T.rt[i],T.rt[i-1],1,inf,a[x]);
        }
        else
        {
            T.rt[i]=T.rt[i-1];
        }
    }
    w[0]=inf+5;
    for(int i=1,u,x,k,v;i<=q;i++)
    {
        scanf("%d%d%d",&u,&x,&k);
        change(u),change(k);
        x=x^ans;
        v=u;
        for(int j=lg;j>=0;j--)if(G.f[v][j]&&w[G.f[v][j]]<=x)v=G.f[v][j];
        if(G.siz[v]<k)ans=-1;
        else ans=T.query(T.rt[G.st[v]-1],T.rt[G.ed[v]],1,inf,k);
        printf("%d\n",ans);
        ans = (ans==-1 ? 0 : ans);
    }
}
int main()
{

    //freopen("Peaks.in","r",stdin);freopen("Peaks.out","w",stdout);
    work();
    return 0;
}

```# [P7834 [ONTAK2010] Peaks 加强版](https://www.luogu.com.cn/problem/P7834)

# [ONTAK2010] Peaks 加强版

## 题目背景

原题链接：[P4197 Peaks](https://www.luogu.com.cn/problem/P4197)

## 题目描述

给定一张 $n$ 个点、$m$ 条边的无向图，第 $i$ 个点的权值为 $a_i$，边有边权。

有 $q$ 组询问，每组询问给定三个整数 $u, x, k$，求从 $u$ 开始只经过权值 $\leq x$ 的边所能到达的权值第 $k$ 大的点的权值，如果不存在输出 $-1$。

**本题强制在线**。

对于 $100\%$ 的数据，$1 \leq n \leq 10^5$，$0 \leq m, q \leq 5 \times 10^5$。


### 说句闲话

感谢著名[未来416之光](https://www.luogu.com.cn/user/527070) @XiaoZi_qwq 的推荐

# Solution:

## 一个很新的东西：kruskal重构树

大概意思就是说，在 **kruskal** 时，对于两个应该连边的点 $(u,v,w)$ ，别急着连边，新建一个点 $x$ 点权为 $w$ 然后连两条边：$x->u,x->v$ 这样建出来的一棵树上，所有叶子节点都由实点构成，两个实点的 $lca$ 的点权就是二者的边权

图的话就借用一下 @asd369 大佬的：
![](https://cdn.luogu.com.cn/upload/image_hosting/kbflkzrt.png)

如图，这是一个最小生成树的 **kruskal** 重构树，它是一个大根堆。

有了这个东西之后这题就好做了：

首先，我们建出 **kruskal** 重构树，然后对它求欧拉序。对于每个询问 $(u,x,k)$ 我们从 $u$ 开始向上倍增直到一个点 $v$ 的点权**严格大于** $x$ 然后我们再在以 $v$ 为根的子树下求第 $k$ 大值就好了

而求第 $k$ 大这显然是主席树的活

需要注意的是我们的主席树是根据欧拉序的第一次访问来顺序建的，只有这样才能满足先祖关系

### 警钟长鸣:
 [注意数据范围以及值域](https://www.luogu.com.cn/record/list?pid=P7834&user=508086)
 # Code:
```cpp
#include<bits/stdc++.h>
const int N=2e5+5;
const int inf=1e9;
const int lg=25;
using namespace std;
int e_cnt,n,m,q,ans;
int a[N],b[N],w[N<<1];
int head[N<<1];
struct Edge{
    int to,nxt;
}e[N<<2];
void add(int x,int y)
{
    e[++e_cnt]={y,head[x]};
    head[x]=e_cnt;
}
struct Kruskal{
    int tot;
    struct edge{
        int u,v,w;
        bool operator <(const edge &e)const{
            return w<e.w;
        }
    }q[N*5];
    int fa[N<<1];
    int find(int x){return fa[x] = fa[x]==x ? fa[x] : find(fa[x]);}
    void build()
    {
        tot=n;
        for(int i=1;i<=n<<1;i++)fa[i]=i;
        for(int i=1;i<=m;i++)scanf("%d%d%d",&q[i].u,&q[i].v,&q[i].w);
        sort(q+1,q+1+m);
        for(int i=1;i<=m;i++)
        {
            int x=find(q[i].u),y=find(q[i].v);
            if(x!=y)
            {
                w[++tot]=q[i].w;
                add(tot,x);add(tot,y);
                fa[tot]=fa[x]=fa[y]=tot;
            }
        }
    }

}K;
struct Grapth{
    int tot=0;
    int f[N<<1][lg+5];
    int siz[N<<1],st[N<<1],ed[N<<1],rid[N<<1];
    void dfs(int x,int fa)
    {
        f[x][0]=fa;
        rid[++tot]=x;st[x]=tot;
        for(int j=1;j<=lg;j++)
        {
            f[x][j]=f[f[x][j-1]][j-1];
        }
        for(int i=head[x];i;i=e[i].nxt)
        {
            int y=e[i].to;
            if(y==f[x][0])continue;
            dfs(y,x);
            siz[x]+=siz[y];
        }
        if(!siz[x])siz[x]=1;
        ed[x]=tot;
    }
}G;
//Segment_Tree
struct Segment_Tree{
    int rt[N<<1];
    int cnt;
    struct Tree{
        int ls,rs,cnt;
    }t[N*80];
    void insert(int &x,int y,int l,int r,int k)
    {
        t[x=++cnt]=t[y];
        t[x].cnt++;
        if(l==r)return;
        int mid=l+r>>1;
        if(k<=mid)insert(t[x].ls,t[y].ls,l,mid,k);
        if(mid<k)insert(t[x].rs,t[y].rs,mid+1,r,k);
    }
    int query(int x,int y,int l,int r,int k)
    {
        if(l==r)return l;
        int Cnt=-t[t[x].rs].cnt+t[t[y].rs].cnt;
        int mid=l+r>>1;
        if(k<=Cnt) return query(t[x].rs,t[y].rs,mid+1,r,k);
        else return query(t[x].ls,t[y].ls,l,mid,k-Cnt);
    }
}T;
void change(int &x)
{
    x=(x^ans)%n + 1;
}
void work()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);b[i]=a[i];
    }
    //sort(b+1,b+1+n);
    //for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+1+n,a[i])-b;
    K.build();
    for(int i=K.tot;i;i--)
    {
        if(!G.siz[i])
        G.dfs(i,0);
    }
    for(int i=1;i<=K.tot;i++)
    {
        int x=G.rid[i];
        if(x<=n)
        {
            T.insert(T.rt[i],T.rt[i-1],1,inf,a[x]);
        }
        else
        {
            T.rt[i]=T.rt[i-1];
        }
    }
    w[0]=inf+5;
    for(int i=1,u,x,k,v;i<=q;i++)
    {
        scanf("%d%d%d",&u,&x,&k);
        change(u),change(k);
        x=x^ans;
        v=u;
        for(int j=lg;j>=0;j--)if(G.f[v][j]&&w[G.f[v][j]]<=x)v=G.f[v][j];
        if(G.siz[v]<k)ans=-1;
        else ans=T.query(T.rt[G.st[v]-1],T.rt[G.ed[v]],1,inf,k);
        printf("%d\n",ans);
        ans = (ans==-1 ? 0 : ans);
    }
}
int main()
{

    //freopen("Peaks.in","r",stdin);freopen("Peaks.out","w",stdout);
    work();
    return 0;
}

```# [P7834 [ONTAK2010] Peaks 加强版](https://www.luogu.com.cn/problem/P7834)

# [ONTAK2010] Peaks 加强版

## 题目背景

原题链接：[P4197 Peaks](https://www.luogu.com.cn/problem/P4197)

## 题目描述

给定一张 $n$ 个点、$m$ 条边的无向图，第 $i$ 个点的权值为 $a_i$，边有边权。

有 $q$ 组询问，每组询问给定三个整数 $u, x, k$，求从 $u$ 开始只经过权值 $\leq x$ 的边所能到达的权值第 $k$ 大的点的权值，如果不存在输出 $-1$。

**本题强制在线**。

对于 $100\%$ 的数据，$1 \leq n \leq 10^5$，$0 \leq m, q \leq 5 \times 10^5$。


### 说句闲话

感谢著名[未来416之光](https://www.luogu.com.cn/user/527070) @XiaoZi_qwq 的推荐

# Solution:

## 一个很新的东西：kruskal重构树

大概意思就是说，在 **kruskal** 时，对于两个应该连边的点 $(u,v,w)$ ，别急着连边，新建一个点 $x$ 点权为 $w$ 然后连两条边：$x->u,x->v$ 这样建出来的一棵树上，所有叶子节点都由实点构成，两个实点的 $lca$ 的点权就是二者的边权

图的话就借用一下 @asd369 大佬的：
![](https://cdn.luogu.com.cn/upload/image_hosting/kbflkzrt.png)

如图，这是一个最小生成树的 **kruskal** 重构树，它是一个大根堆。

有了这个东西之后这题就好做了：

首先，我们建出 **kruskal** 重构树，然后对它求欧拉序。对于每个询问 $(u,x,k)$ 我们从 $u$ 开始向上倍增直到一个点 $v$ 的点权**严格大于** $x$ 然后我们再在以 $v$ 为根的子树下求第 $k$ 大值就好了

而求第 $k$ 大这显然是主席树的活

需要注意的是我们的主席树是根据欧拉序的第一次访问来顺序建的，只有这样才能满足先祖关系

### 警钟长鸣:
 [注意数据范围以及值域](https://www.luogu.com.cn/record/list?pid=P7834&user=508086)
 # Code:
```cpp
#include<bits/stdc++.h>
const int N=2e5+5;
const int inf=1e9;
const int lg=25;
using namespace std;
int e_cnt,n,m,q,ans;
int a[N],b[N],w[N<<1];
int head[N<<1];
struct Edge{
    int to,nxt;
}e[N<<2];
void add(int x,int y)
{
    e[++e_cnt]={y,head[x]};
    head[x]=e_cnt;
}
struct Kruskal{
    int tot;
    struct edge{
        int u,v,w;
        bool operator <(const edge &e)const{
            return w<e.w;
        }
    }q[N*5];
    int fa[N<<1];
    int find(int x){return fa[x] = fa[x]==x ? fa[x] : find(fa[x]);}
    void build()
    {
        tot=n;
        for(int i=1;i<=n<<1;i++)fa[i]=i;
        for(int i=1;i<=m;i++)scanf("%d%d%d",&q[i].u,&q[i].v,&q[i].w);
        sort(q+1,q+1+m);
        for(int i=1;i<=m;i++)
        {
            int x=find(q[i].u),y=find(q[i].v);
            if(x!=y)
            {
                w[++tot]=q[i].w;
                add(tot,x);add(tot,y);
                fa[tot]=fa[x]=fa[y]=tot;
            }
        }
    }

}K;
struct Grapth{
    int tot=0;
    int f[N<<1][lg+5];
    int siz[N<<1],st[N<<1],ed[N<<1],rid[N<<1];
    void dfs(int x,int fa)
    {
        f[x][0]=fa;
        rid[++tot]=x;st[x]=tot;
        for(int j=1;j<=lg;j++)
        {
            f[x][j]=f[f[x][j-1]][j-1];
        }
        for(int i=head[x];i;i=e[i].nxt)
        {
            int y=e[i].to;
            if(y==f[x][0])continue;
            dfs(y,x);
            siz[x]+=siz[y];
        }
        if(!siz[x])siz[x]=1;
        ed[x]=tot;
    }
}G;
//Segment_Tree
struct Segment_Tree{
    int rt[N<<1];
    int cnt;
    struct Tree{
        int ls,rs,cnt;
    }t[N*80];
    void insert(int &x,int y,int l,int r,int k)
    {
        t[x=++cnt]=t[y];
        t[x].cnt++;
        if(l==r)return;
        int mid=l+r>>1;
        if(k<=mid)insert(t[x].ls,t[y].ls,l,mid,k);
        if(mid<k)insert(t[x].rs,t[y].rs,mid+1,r,k);
    }
    int query(int x,int y,int l,int r,int k)
    {
        if(l==r)return l;
        int Cnt=-t[t[x].rs].cnt+t[t[y].rs].cnt;
        int mid=l+r>>1;
        if(k<=Cnt) return query(t[x].rs,t[y].rs,mid+1,r,k);
        else return query(t[x].ls,t[y].ls,l,mid,k-Cnt);
    }
}T;
void change(int &x)
{
    x=(x^ans)%n + 1;
}
void work()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);b[i]=a[i];
    }
    //sort(b+1,b+1+n);
    //for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+1+n,a[i])-b;
    K.build();
    for(int i=K.tot;i;i--)
    {
        if(!G.siz[i])
        G.dfs(i,0);
    }
    for(int i=1;i<=K.tot;i++)
    {
        int x=G.rid[i];
        if(x<=n)
        {
            T.insert(T.rt[i],T.rt[i-1],1,inf,a[x]);
        }
        else
        {
            T.rt[i]=T.rt[i-1];
        }
    }
    w[0]=inf+5;
    for(int i=1,u,x,k,v;i<=q;i++)
    {
        scanf("%d%d%d",&u,&x,&k);
        change(u),change(k);
        x=x^ans;
        v=u;
        for(int j=lg;j>=0;j--)if(G.f[v][j]&&w[G.f[v][j]]<=x)v=G.f[v][j];
        if(G.siz[v]<k)ans=-1;
        else ans=T.query(T.rt[G.st[v]-1],T.rt[G.ed[v]],1,inf,k);
        printf("%d\n",ans);
        ans = (ans==-1 ? 0 : ans);
    }
}
int main()
{

    //freopen("Peaks.in","r",stdin);freopen("Peaks.out","w",stdout);
    work();
    return 0;
}