P5039 [SHOI2010] 最小生成树

P5039 [SHOI2010] 最小生成树

[SHOI2010] 最小生成树

题目描述

Secsa最近对最小生成树问题特别感兴趣。他已经知道如果要去求出一个 $ n $ 个点、 $ m $ 条边的无向图的最小生成树有一个Krustal算法和另一个Prim的算法。另外，他还知道，某一个图可能有多种不同的最小生成树。例如，下面图3中所示的都是图2中的无向图的最小生成树：

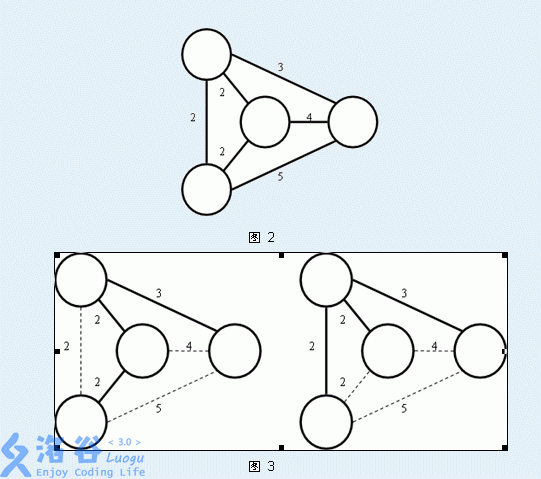
当然啦，这些都不是今天需要你解决的问题。Secsa想知道对于某一条无向图中的边AB，至少需要多少代价可以保证AB边在这个无向图的最小生成树中。为了使得AB边一定在最小生成树中，你可以对这个无向图进行操作，一次单独的操作是指：先选择一条图中的边 P1P2，再把图中除了这条边以外的边，每一条的权值都减少 $ 1 $ 。如图4所示就是一次这样的操作：

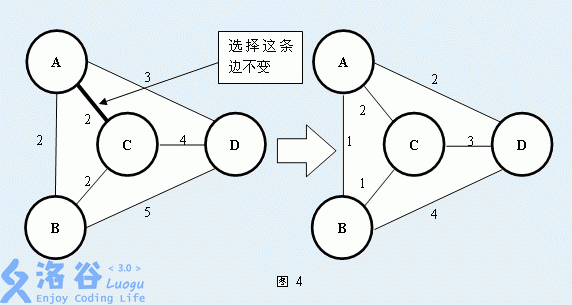
输入格式

输入文件的第一行有3个正整数 $ n,m,Lab $ 分别表示无向图中的点数、边数、必须要在最小生成树中出现的AB边的标号。

接下来 $ m $ 行依次描述标号为 $ 1,2,3 \ldots m $ 的无向边，每行描述一条边。每个描述包含3个整数 $ x,y,d $ ，表示这条边连接着标号为 $ x,y $ 的点，且这条边的权值为 $ d $ 。

输入文件保证 $ 1 \leq x,y \leq N $ ， $ x \neq y $ ，且输入数据保证这个无向图一定是一个连通图。

输出格式

输出文件只有一行，这行只有一个整数，即，使得标号为 $ Lab $ 边一定出现最小生成树中的最少操作次数。

提示

$ 1 \leq N \leq 500,1 \leq M \leq 800,1 \leq d<10^6 $

Solution:

首先，拿到题目先读数据范围：$ 1 \leq N \leq 500 ！！！$
这令我们很难不想到网络流，但是我们先别急，看看题目到底要我们干什么：

我们回忆一下kurskal在干什么：对于所有边排序，从小到大遍历每条边，如果该边的两个端点不在同一联通快内，则将他们连接起来，那么一条边AB保证能加入最小生成树的充要条件就是在将所有边权小于等于AB的边构造一张图后，A,B两点不连通

“再把图中除了这条边以外的边，每一条的权值都减少 $ 1 $”
这个操作显然等价于将u->v这一条边的权值加 \(1\)

由于题目又提示我们这题的数据范围十分网络流，所以我们不妨大胆转化一下题目：

将A视作源点，B点视作汇点，对于每一条满足\(w[j] \leq w[AB]\)的边，在网络中建一条以边j的端点为端点，权值为(w[AB]-w[j]+1)的双向边，然后对于此网络跑一个最小割，正确性是显然的

然后这题就做完了

国庆集训能场切这种题也是十分开心的

Code:

#include<bits/stdc++.h>
const int N=805;
const int inf=1e9;
using namespace std;
struct Edge{
    int to,nxt,fl;
}e[N<<2];
int n,m,e_cnt=1,S,T,W,ans,k;
int head[N];
void add(int x,int y,int fl)
{
    //cout<<x<<" "<<y<<" "<<fl<<"\n";
    e[++e_cnt]=(Edge){y,head[x],fl};head[x]=e_cnt;
    e[++e_cnt]=(Edge){x,head[y],0};head[y]=e_cnt;
}
struct  kkk{
    int x,y,w;
    bool operator <(const kkk &k)const{
        return w<k.w;
    }
}q[N];
int dis[N],pre[N],pre_id[N],dl[N],flow[N];
void init()
{
    for(int i=1;i<=n;i++)
    {
        dis[i]=inf;
        dl[i]=0;
        flow[i]=0;
    }
}
queue<int> Q;
bool spfa(int s,int t)
{
    init();
    dis[s]=0;Q.push(s);dl[s]=1;
    flow[s]=inf;
    while(!Q.empty())
    {
        int u=Q.front();Q.pop();
        dl[u]=0;
        //cout<<"u:"<<u<<" "<<dis[u]<<"="<<flow[u]<<"\n";
        for(int i=head[u],v,fl;i;i=e[i].nxt)
        {
            v=e[i].to,fl=e[i].fl;
            if(fl&&dis[v]>dis[u]+1)
            {
                dis[v]=dis[u]+1;
                flow[v]=min(flow[u],fl);
                pre[v]=u;pre_id[v]=i;
                if(!dl[v])
                {
                    Q.push(v);
                    dl[v]=1;
                }
            }
        }
    }
    //cout<<"flow:"<<flow[t]<<"\n";
    return flow[t];
}
void dinic()
{
    while(spfa(S,T))
    {
        int now=T,fl=flow[T];ans+=flow[T];
        while(now!=S)
        {
            int i=pre_id[now];
            e[i].fl-=fl;
            e[i^1].fl+=fl;
            now=pre[now];
        }
    }
}
void work()
{
    cin>>n>>m>>k;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&q[i].x,&q[i].y,&q[i].w);
    }
    S=q[k].x,T=q[k].y,W=q[k].w+1;
    sort(q+1,q+1+m);
    for(int i=1;i<=m&&q[i].w<W;i++)
    {
        if(q[i].x==q[i].y)continue;
        if(q[i].x==S&&q[i].y==T)continue;
        add(q[i].x,q[i].y,W-q[i].w);
        add(q[i].y,q[i].x,W-q[i].w);
    }
    dinic();
    printf("%d\n",ans);
}
int main()
{
    //freopen("tree.in","r",stdin);
    //freopen("tree.out","w",stdout);
    work();
    return 0;
}