P3623 [APIO2008] 免费道路
P3623 [APIO2008] 免费道路
[APIO2008] 免费道路
题目描述
新亚(New Asia)王国有 N 个村庄,由 M 条道路连接。其中一些道路是鹅卵石路,而其它道路是水泥路。保持道路免费运行需要一大笔费用,并且看上去 王国不可能保持所有道路免费。为此亟待制定一个新的道路维护计划。
国王已决定保持尽可能少的道路免费,但是两个不同的村庄之间都应该一条且仅由一条 且仅由一条免费道路的路径连接。同时,虽然水泥路更适合现代交通的需 要,但国王也认为走在鹅卵石路上是一件有趣的事情。所以,国王决定保持刚好 K 条鹅卵石路免费。
举例来说,假定新亚王国的村庄和道路如图 3(a)所示。如果国王希望保持两 条鹅卵石路免费,那么可以如图 3(b)中那样保持道路(1, 2)、(2, 3)、(3, 4)和(3, 5) 免费。该方案满足了国王的要求,因为:(1)两个村庄之间都有一条由免费道 路组成的路径;(2)免费的道路已尽可能少;(3)方案中刚好有两条鹅卵石道路 (2, 3)和(3, 4)
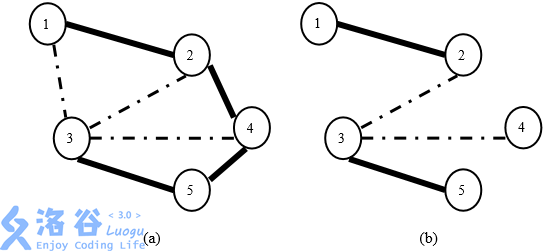
图 3: (a)新亚王国中村庄和道路的一个示例。实线标注的是水泥路,虚线标注 的是鹅卵石路。(b)一个保持两条鹅卵石路免费的维护方案。图中仅标出了免费道路。
给定一个关于新亚王国村庄和道路的述以及国王决定保持免费的鹅卵石 道路数目,写一个程序确定是否存在一个道路维护计划以满足国王的要求,如果 存在则任意输出一个方案。
Solution:
首先我们通过观察题目中:
(1)两个村庄之间都有一条由免费道 路组成的路径;(2)免费的道路已尽可能少
这两句话不难发现这是一个生成树问题:有两种边:0/1
然后要求你这颗生成树的总权值是k(注意这里的0/1和题目中的0/1恰巧相反,要注意在输入和输出时取反)
我们不难想到用kruskal解决:
首先跑一个只有0边的生成树,得到一个或者多个集合,显然这些集合间需要1边进行链接,把这些1边记录下来
然后就是这题的重点:
本蒟蒻想了三节课都没想通的地方·被dalao的题解30s解决了
在求出这些必须的1边之后,可能1边的总数cnt并未到达k:
我们先将生成树还原回单点,然后先加必须的1边,再加其他的1边使得cnt=k.然后剩下的边用0边补全
最后补一下无解的情况:
1:这个图本身不连通
2: 再进行第二次kruskal之后cnt!=k
然后这题就写完了
Code:
#include<bits/stdc++.h> const int N=1e5+5; using namespace std; int fa[N]; int n,m,k,cnt,tot[2],num; int find(int x){fa[x]=fa[x]==x ? fa[x] : find(fa[x]);return fa[x];} int u[2][N],v[2][N]; vector<int> ans[2]; void init() { for(int i=1;i<=n;i++){fa[i]=i;} } void work() { cin>>n>>m>>k; init(); for(int i=1,x,y,w;i<=m;i++) { scanf("%d%d%d",&x,&y,&w); w^=1; u[w][++tot[w]]=x; v[w][tot[w]]=y; } for(int i=1;i<=tot[0];i++) { int x=find(u[0][i]),y=find(v[0][i]); if(x!=y) { fa[y]=x; num++; } } for(int i=1;i<=tot[1];i++) { int x=find(u[1][i]),y=find(v[1][i]); if(x!=y) { fa[y]=x; ans[1].push_back(i); cnt++; } } if(num+cnt!=n-1) { cout<<"no solution"; return ; } init(); for(int id=0;id<ans[1].size();id++) { int i=ans[1][id]; int x=find(u[1][i]),y=find(v[1][i]); fa[y]=x; } for(int i=1;i<=tot[1]&&cnt<k;i++) { int x=find(u[1][i]),y=find(v[1][i]); if(x!=y) { fa[y]=x; ans[1].push_back(i); cnt++; } } if(cnt!=k) { cout<<"no solution"; return ; } for(int i=1;i<=tot[0];i++) { int x=find(u[0][i]),y=find(v[0][i]); if(x!=y) { fa[y]=x; ans[0].push_back(i); } } for(int id=0;id<ans[0].size();id++){int i=ans[0][id];printf("%d %d %d\n",u[0][i],v[0][i],1);} for(int id=0;id<ans[1].size();id++){int i=ans[1][id];printf("%d %d %d\n",u[1][i],v[1][i],0);} } int main() { freopen("P3623.in","r",stdin);freopen("P3623.out","w",stdout); work(); return 0; }



