杂题选写

建造军营

记得当时是抄的题解，现在感觉真的很显然。

显然在一个边双里面任意选择都是无限制的，所以直接缩点然后建出树，直接树 dp。

考虑子树内的贡献，发现一旦子树内有任何一个点被选就要考虑连通性。所以设 \(dp(i,0/1)\) 表示里面是否选择过点。

转移显然（如果里面有点，并且要外面新加点要合法的话就必须把边选上），初始化显然。考虑统计答案。

显然不是 \(dp(1,1)\)，因为此时强制了 1 的连通块内的树边都要选，这显然是不完全的。

所以你枚举 x，钦定这个点是连通块最上面汇集的点即可。

为了避免算重，需要让 x->fa 的边不选（否则和 fa 统计重复），那么子树外面的边随便选即可。

信号传递

题意真的不是很清楚。

S 序列不变，你要改变的是 S 中每个元素的坐标位置。

所以我们状压转移就默认按照坐标位置加入即可。（也就是对于 \(S\)，新加入一个点 \(x\)，\(S\) 中的点在位置 \([1,popcount(S)]\)，\(x\) 的位置是 \(popcount(S)+1\)）

考虑贡献，\(S\rightarrow i\) 的代价是显然的（第一类）。考虑第二类。

稍微卡一下空间即可。

季风

结论 1

\(x'_i\) 必然同号，\(y'_i\) 同理。

证明：把 [0,m) 的 x',y' 任意分配后， 任意 x' 和 y' 相对独立；所以 x' only 和 x 有关了。

得到：

\[|X-\sum x_i|+|Y-\sum y_i|\le mk \]

不妨 \(m=tn+p\)。

一种做法是直接拆绝对值对于每种情况求出 \(t\) 的范围，看是否有解。参考代码：https://www.becoder.com.cn/submission/2382821 。（可能也不是特别复杂？）

更巧妙的做法是考虑 4 个式子，你不管这个式子是不是对的，都求出 \(t\) 的范围，最后取个交即可。

为什么是对的？ddxrS 解释道每个式子左边的值取到上界当且仅当满足这个式子的前提条件。

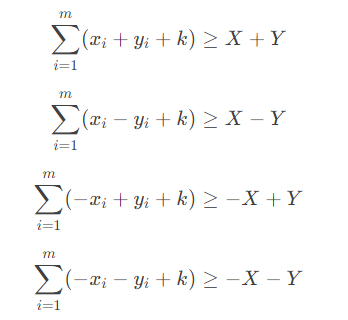
上面 4 种情况，比如说 \(\sum x_i \le X,\sum y_i\le Y\) 的时候有第一个，那么你此时直接带入另外 3 个，发现一定成立。

其它的也是类似，证毕。

下面开始解：例如当两个绝对值前面取正后面取负：

\[X-Y-\sum x_i+\sum y_i\le mk \]

\[X-Y-(t\times all_x+p1_i)+(t\times all_y+p2_i)\le (tn+i)k \]

\[X-Y-p1_i+p2_i-ik\le(nk+all_x-all_y)t \]

可以解出 \(t\) 的范围。

还好很快就调出来了，不然真的破防了兄弟。代码

回文

这个思想在很多题都有用，比如双序列。

考虑每次选择一个数 \((x,p1)\)，那么我们就可以确定 \((x,p2)\) 的操作时间了。

考虑第一次，以左边为例。原序列分成了剩下的 2 个部分：\([2,p1),(p1,n]\)。注意到左右先后取的关系是类似栈的形式。

然后再手玩一下发现每次可以操作当且仅当栈顶等于栈底，2 个栈排列组合即可，证明简单。做完了。