8.6 矩阵？

在这之前，我们先刷一下 CF。

1 CF

1.1 CF1997E (edu168)

注意到每个 \(k\) 只会升 \(n/k\) 次级，那么总的升级次数就是调和级数，是 \(O(n\log n)\)。

每次升级二分+数据结构 log^2 算。3log。

考虑每个位置，由于单调性，直接二分出分界值。配合 bit 2log。

然而可以在 bit 上用倍增来二分，单 log。

1.2 CF1997F

题还没看懂。sb

1.3 CF1993C (963d2)

感觉算有意思。

• \(s\ge \max a_i\)

• \(s\bmod 2k\) 在所有区间的交上。

区间：\([a_i\bmod 2k,(a_i+k-1)\bmod 2k]\)。

可以找到 \(s\bmod 2k\) 的最小值确定 \(s\) 的最终值，two pointers。

有个 corner case：如何知道当前区间包含了所有线段。考虑移动 \(l,r\) 的时候更新这个位置的 \(a_i\) 的 cnt。

1.4 CF1993D

二分中位数，就是要剩下的连续段 sum 非负。

然后 dp 是吗，设计某个位置之前的大和。转移简单。但是是 2 维的，怎么优化？

要挖掘一些性质了。

特殊在于每次删的长度都是 \(k\)，我们考虑保留下来的 \(i_1,i_2,...,i_m\)。

在模 \(k\) 意义下应该是递增的。（考察注意力）

然后就可以 1 维 dp 了。挺妙的。

---

2 矩阵

2.1 CF1970E3

首先是有一个比较平凡的 dp，可以过 E2。

发现转移是 \(m^3\) 的，非常耗时。

那么只能在矩阵上操作。

Trick：可以将转移矩阵拆成 2 个矩阵相乘，利用结合律将行列翻转。使得转移矩阵变小。

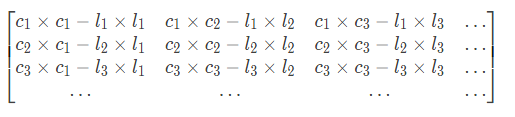
转移矩阵 \(T=AB\)，\(A=n*2,B=2*n\)。

结合律：\(ABC=A(BC)\)。

要求 \((AB)^n = (AB)(AB)(AB)...(AB) = A (BA)(BA)...(BA)B= A(BA)^{n-1}B\)。

发现 \(BA\) 是 \(2*2\) 的。可以转移。

2.2 CF1609E

就是个线段树，也可以弄成 min + 的矩乘放 ds 上。

2.3 CF51E

5=2+3，枚举中间点。不知道和矩阵由什么关系。

注意处理 3 元环 + 一条边来回的情况。

2.4 CF1458C

矩阵乘法维护操作。逆排列有趣。

对于每个数，考虑维护每次操作对这一个数的变化量。由于形式一直，维护 1 个即可，最后再对每一个位置还原。

维护 \([val,i,j,1]\)。\(1\) 用来处理下标平移。

逆排列就是把 \(id\) 和 \(val\) 交换，很好啊。

2.5 CF837F

首先按照尝试感觉多次前缀和的增长会特别地快。

尝试构造增长最慢的数据：（可以去前导 0）

11 10000000000000000
1 0 0 0 0 0 0 0 0 0 1

跑出来是 282。

那么 \(n\) 很大的时候就一直跑即可，这个次数一定是很小的，大概到 10 就行。

次数很小严谨来说考虑组合意义。设 \(f_{i,j}\) 表示第 \(i\) 轮，则转移是 \(f_{i,j}=f_{i-1,j-1}+f_{i-1,j}\)，就是杨辉三角组合数，所以很大。。。

考虑 \(n\le 10\)，由于次数和 \(n\) 不是同级所以需要矩阵快速幂加速前缀和，再套个二分即可。

2.6 CF593E

sb 题。

好像还是有点难度，套路地对于每个阶段都跑一遍矩乘即可。

2.7 P2151

不能走重复的边很烦，那么就设状态表示走到 \(j\) 的末尾点。

2.8 P5303

对绅士的代码表示震惊。

好吧我也是这样……

/*
[i][S][3] 表示，这一块的状态，现在还有几块空余块 
S 是常数 :
0: 竖着的
1: 上面单个，下面横开始
2:				   结束
3: 上面横开始，下面单个
4: 上面横结束，下面单个
5: 上面横开始，下面横开始 
6: 上面横开始，下面横结束
7: 上面横结束，下面横开始
8: 上面横结束，下面横结束

那么一共就只有 27 种状态。代码非常好写，亿会就写完了。 
*/