5.5 最大前缀和 & 时间流逝 & 树上异或

注意：暴力是 $n!$ 的，不是指数。

马上就想到了假设当前选数状态是一个前缀的方案数，应该是 $f_i\times g_{S-i}$。

考虑计算 $f$ 和 $g$。利用一些性质，简单计算即可……

需要注意的是 $f$ 的转移，如果是【将 $a_i$ 放在最后】不好转移，于是我们考虑把他放到最前面。

---

形式化题意

给定一长为 $N$ 的有序序列 $a$，序列内元素两两不同。你现在有一个栈，初始为空，你会不断执行以下操作直到栈内元素之和 $>T$。一次「操作」过程如下：

• 如果栈不为空，则有 $P$ 的概率弹出一个元素。

• 如果没弹，在所有 $\le$ 栈顶的 $a_i$ 里随机地取一个，将其入栈（不把 $a_i$​ 删掉，下一次也可能继续入栈）。

问操作终止时进行操作次数的期望。

Sol

首先考虑状态树。是一个单调递减的状态，并且和很小。这个状态数考试的时候要去搜一下，如果可以接受就直接搞。结论：在 ${10}^6$ 左右。

假设根节点为 $\varnothing$。则 $f_i=P\times (f_{fa}+1)+{\displaystyle \frac{1-P}{i{n}_i}}\times \sum (f_{to}+1)$。

注意这里的概率都是 $i$ 这个点的，不能弄成其它。比如 $f_{fa}+1$ 表示 $i$ 走一步可以到 $fa$。

【树上高斯消元】：其实就是将这个式子后效性去除。

设 $f_x=k_x\times f_{fa}+b_x$，带进去每次转移的时候一下算下 $k,b$ 即可。

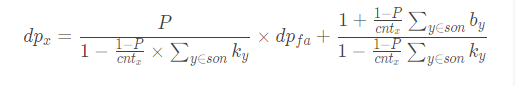
注意到这是一个线性关系，我们根本就不需要知道 $dp$ 的值，只需每次回溯 $k,b$ 最后线性推出。

此题更特殊，因为根节点 $P=0$，所以 $d{p}_1=b_1$。

---

P9745 一道非常好的树上 dp

树上问题可以先考虑链的情况。

链的话就是一个 $n^2$ dp。钦定当前第一次断。

这个题的状态定义非常的妙，记住！！！

首先注意到：$x=\sum \prod ⨁$ 在加入一个新的 ${⨁}^{\prime }$ 后，答案为 $x\times {⨁}^{\prime }$。

注意题目是【联通块删边】。因此普通的状态不行。设 $f(i,S)$ 表示当前和 $i$ 相连的块 xor 和为 $S$，其余的块的异或乘积的和。注意还有个 其余的块。

这个状态的优势在于：你每次算一条边，如果不删，那么可以直接和 $S$ 进行背包转移；如果删，那么跟 $i$ 的块没有任何影响，只是更新即可。

因此还需要记录一个真正的 $dp(i)$ 表示 $i$ 子树的答案，处理【删边】的情况。

并且我们当前已经知道 $i$ 所在块的状态，所以只记录其他的会更方便。

故 $f(i,S)=f(i,S)\times dp(to)+\sum f(i,S⨁x)\times f(to,x)$

后面的转移是不删边，由于计算的不包含 $i$，所以把另外两块独立的乘起来即可。

$g$ 转移显然。

然后考虑优化，应该可以看出来要拆位。$f(i,j,0/1)$。

然后你发现后面的转移就是把 $S$ 给二进制分解，做一做即可。

但是为什么拆位算出来是对的。考虑 $dp$ 的转移，这显然是没有问题的。

反正记住异或可以拆位就行了，合并应该都适用。

#include <bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int N = 5e5 + 5, M = 63, Mod = 998244353; ll read();
int n, m; vector <int> G[N];
ll a[N];
int dp[N], f[N][M][2];

void dfs(int x, int fa) {
	// init x only 具体来说，是和 x 结合乘了多少 
	for(int i = 0;i <= 61; ++i)
		if(a[x] & (1ll << i)) f[x][i][1] = 1;
		else f[x][i][0] = 1;
	for(int to : G[x]) {
		if(to == fa) continue ;
		dfs(to, x);
		for(int j = 0;j <= 61; ++j) {
			int xx = f[x][j][1], y = f[x][j][0];
f[x][j][1] = (1ll * xx * dp[to] % Mod + 1ll * y * f[to][j][1] % Mod + 1ll * xx * f[to][j][0] % Mod) % Mod;
f[x][j][0] = (1ll * y * dp[to] % Mod + 1ll * xx * f[to][j][1] % Mod + 1ll * y * f[to][j][0] % Mod) % Mod;
		}
	}
	for(int j = 0;j <= 61; ++j) dp[x] = (dp[x] + (1ll << j) % Mod * 1ll * f[x][j][1] % Mod) % Mod;
}
// dp(x) = \sum f(x, y) * y 其它子树内连通块异或和的乘积。
// 具体地，你的拆位只是当一个状态变化 
signed main() {
	cin >> n;
	for(int i = 1;i <= n; ++i) a[i] = read();
	for(int i = 2, x;i <= n; ++i) {
		x = read(); 
		G[x].pb(i), G[i].pb(x); 
	} dfs(1, 0);
	cout << dp[1];
    return 0;
}
ll read() {
	char c; ll f = 1, sum = 0;
	while(c < '0' or c > '9') {if(c == '-') f = -1;c = getchar();}
	while(c >= '0' and c <= '9') {sum = (sum << 3) + (sum << 1) + (c ^ 48);c = getchar();} 
	return sum * f;
}
// f(i, j, 0) = f(i,j,0)*g(to) + f(i,j,0)*f()
// 每一位的单独情况