分支限界法(四)——旅行售货员问题(转)
来自:http://www.cnblogs.com/chinazhangjie/archive/2010/11/08/1871873.html
1. 问题描述
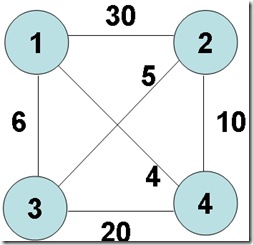
某售货员要到若干城市去推销商品,已知各城市之间的路程(或旅费)。他要选定一条从驻地出发,经过每个城市一次,最后回到驻地的路线,使总的路程(或总旅费)最小。
路线是一个带权图。图中各边的费用(权)为正数。图的一条周游路线是包括V中的每个顶点在内的一条回路。周游路线的费用是这条路线上所有边的费用之和。
旅行售货员问题的解空间可以组织成一棵树,从树的根结点到任一叶结点的路径定义了图的一条周游路线。旅行售货员问题要在图G中找出费用最小的周游路线(解空间:排列树)。
2. 算法描述
算法开始时创建一个最小堆,用于表示活结点优先队列。堆中每个结点的子树费用的下界lcost值是优先队列的优先级。接着算法计算出图中每个顶点的最小费用出边并用minout记录。
如果所给的有向图中某个顶点没有出边,则该图不可能有回路,算法即告结束。如果每个顶点都有出边,则根据计算出的minout作算法初始化。
使用最小堆:
对树中的每个节点,定义以下成员变量:
优先级:lcost
当前节点的路径长度:cc
剩余节点的最小出边和:rcost
节点在树中的深度:s
长度为n的数组x[0:n-1],用来存放从起点开始的路径。
我们定义:
对第n-2层以上的节点:lcost = cc + rcost
对第n-1,n-2层的节点:lcost = 该回路的长度
算法的while循环体完成对排列树内部结点的扩展。对于当前扩展结点,算法分2种情况进行处理:
1、首先考虑s = n-2的情形,此时当前扩展结点是排列树中某个叶结点的父结点。如果该叶结点相应一条可行回路且费用小于当前最小费用,即:lcost < bestc,则将该叶结点插入到优先队列中,否则舍去该叶结点。
2、当s < n-2时,算法依次产生当前扩展结点的所有儿子结点。由于当前扩展结点所相应的路径是x[0:s],其可行儿子结点是从剩余顶点x[s+1:n-1]中选取的顶点x[i],且(x[s],x[i])是所给有向图G中的一条边。对于当前扩展结点的每一个可行儿子结点,计算出其前缀(x[0:s],x[i])的费用cc和相应的下界lcost。当lcost<bestc时,将这个可行儿子结点插入到活结点优先队列中。
算法中while循环的终止条件:
当s=n-1时,相应的扩展结点表示一个叶结点。已找到的回路前缀是x[0:n-1],它已包含图G的所有n个顶点。
此时该叶结点所相应的回路的费用等于cc和lcost的值。剩余的活结点的lcost值不小于已找到的回路的费用。它们都不可能导致费用更小的回路。因此已找到的叶结点所相应的回路是一个最小费用旅行售货员回路,算法可以结束。
实现
/* 主题:旅行售货员问题
* 作者:chinazhangjie * 邮箱:chinajiezhang@gmail.com * 开发语言:C++ * 开发环境:Microsoft Virsual Studio 2005 * 时间: 2010.11.10 */ #include <iostream> #include <vector> #include <queue> #include <limits> using namespace std ; class heap_node { public: heap_node (float lc, float cc, float rc, int s, const vector<int>& p) : lower_cost (lc), current_cost (cc), remainder_cost (rc), size(s) { path = p ; } friend bool operator < (const heap_node& rhs, const heap_node& lhs) { return rhs.lower_cost > lhs.lower_cost ; } public: float lower_cost ; // 子树费用的下界 float current_cost ; // 当前费用 float remainder_cost ;// 剩余顶点的最小出边费用和 int size ; // 根节点到当前结点的路径为path [0 : s] vector<int> path ; // 需要进一步搜索的顶点是path [s+1 : n-1] } ; class BBTSP { public: static float MAX_VALUE; static float NO_EDGE_VALUE; typedef priority_queue<heap_node> min_heap ; public: // 构造函数 BBTSP (const vector<vector<float> >& g) { graph = g ; node_count = (int)g.size (); best_p.resize (node_count) ; } void bb_TSP () { int n = node_count; min_heap mh ; // 最小堆 // min_out[i] = 顶点i最小出边费用 vector<float> min_out(node_count) ; float min_sum = 0.0f ; // 最小出边费用和 for (int i = 0; i < node_count ; ++ i) { float min = MAX_VALUE ; for (int j = 0; j < node_count ; ++ j) { if (graph[i][j] != NO_EDGE_VALUE && graph[i][j] < min) { min = graph[i][j] ; } } if (min == MAX_VALUE) { cerr << " No cycle !" << endl; return ; } min_out[i] = min ; min_sum += min ; } for (int i = 0; i < node_count ; ++ i) { cout << "结点" << i << "的最小出边费用和为: " << min_out[i] << endl ; } cout << "总出边费用为: " << min_sum << endl << endl ; // 初始化 vector<int> path(n) ; for (int i = 0; i < n; ++ i) { path[i] = i; } heap_node hn(0, 0, min_sum, 0, path); float best_c = MAX_VALUE ; // 搜索排列空间树 while (hn.size < n - 1) { // 非叶结点 path = hn.path ; cout << "path: " ; copy (path.begin(), path.end(), ostream_iterator<int>(cout,"")) ; cout << endl ; if (hn.size == n - 2) { // 当前扩展结点是叶结点的父结点 // 再加条边构成回路 // 所构成的回路是否优于当前最优解 if (graph[path[n-2]][path[n-1]] != NO_EDGE_VALUE && graph[path[n-1]][1] != NO_EDGE_VALUE && hn.current_cost + graph[path[n-2]][path[n-1]] + graph[path[n-1]][1] < best_c ) { // 找到费用更小的回路 best_c = hn.current_cost + graph[path[n-2]][path[n-1]] + graph[path[n-1]][1] ; hn.current_cost = best_c ; hn.lower_cost = best_c ; hn.size ++ ; mh.push (hn) ; } } else { // 产生当前扩展结点的儿子结点 for (int i = hn.size + 1; i < n; ++ i) { if (graph[path[hn.size]][path[i]] != NO_EDGE_VALUE) { // 可行的儿子结点 float cc = hn.current_cost + graph[path[hn.size]][path[i]] ; float rcost = hn.remainder_cost - min_out[path[hn.size]] ; // 优先级= 当前费用+ 剩余结点的最小费用和- 当前节点的最小费用 float b = cc + rcost ; // 下界 if (b < best_c) { // 子树可能含最优解,结点插入最小堆 vector<int> p(n) ; for (int j = 0; j < n; ++ j) { p[j] = path[j] ; } //copy (p.begin(), p.end(), ostream_iterator<int> (cout, " ")) ; //cout << ", " ; p[hn.size + 1] = path[i] ; p[i] = path[hn.size + 1] ; //copy (p.begin(), p.end(), ostream_iterator<int> (cout, " ")) ; //cout << endl; heap_node in(b, cc, rcost, hn.size + 1, p) ; mh.push (in) ; } } } } // 取下一扩展结点 hn = mh.top () ; mh.pop () ; } best_cost = best_c ; for (int i = 0; i < node_count; ++ i) { best_p[i] = path[i] ; } copy (best_p.begin(), best_p.end(), ostream_iterator<int> (cout, "")) ; cout << endl ; cout << "best cost : " << best_cost << endl ; } private: vector<vector<float> > graph ; // 图的数组表示 int node_count ;// 结点个数 vector<int> best_p ; // 产生最优解的路径 float best_cost ; // 最优解 } ; float BBTSP::MAX_VALUE = numeric_limits<float>::max() ; float BBTSP::NO_EDGE_VALUE = -1.0f ; int main() { // 图的初始化 const int size = 6 ; vector<vector<float> > g(size) ; for (int i = 0; i < size; ++ i) { g[i].resize (size) ; } for (int i = 0;i < size; ++ i) { g[i][i] = BBTSP::NO_EDGE_VALUE ; } g[0][1] = 30 ; g[0][2] = 6 ; g[0][3] = 4 ; g[0][4] = 5 ; g[0][5] = 6 ; g[1][0] = 30 ; g[1][2] = 4 ; g[1][3] = 5 ; g[1][4] = 2 ; g[1][5] = 1 ; g[2][0] = 6 ; g[2][1] = 4 ; g[2][3] = 7 ; g[2][4] = 8 ; g[2][5] = 9 ; g[3][0] = 4 ; g[3][1] = 5 ; g[3][2] = 7 ; g[3][4] = 10 ; g[3][5] = 20 ; g[4][0] = 5 ; g[4][1] = 2 ; g[4][2] = 8 ; g[4][3] = 10 ; g[4][5] = 3 ; g[5][0] = 6 ; g[5][1] = 1 ; g[5][2] = 9 ; g[5][3] = 20 ; g[5][4] = 3 ; BBTSP bt(g) ; bt.bb_TSP () ; return 0 ; }
运行结果:
 代码
代码
结点 1的最小出边费用和为: 1
结点 2的最小出边费用和为: 4
结点 3的最小出边费用和为: 4
结点 4的最小出边费用和为: 2
结点 5的最小出边费用和为: 1
总出边费用为: 16
path: 012345
path: 032145
path: 042315
path: 031245
path: 041325
path: 031542
path: 041523
path: 021345
path: 031425
path: 052341
path: 045312
path: 051342
path: 045132
path: 021345
path: 021543
path: 031542
path: 051432
path: 021435
path: 032145
path: 031452
path: 032145
path: 032154
path: 021543
path: 021453
path: 041235
path: 054321
path: 031245
path: 054123
path: 032145
path: 051243
051243
best cost : 21






 浙公网安备 33010602011771号
浙公网安备 33010602011771号