113. Path Sum II
题目

分析:
主要考察二叉树深度优先遍历(DFS),递归调用当前节点的左右结点即可,代码如下(copy网上):
1 /** 2 * Definition for binary tree 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 private: 12 vector<vector<int> > ret; 13 public: 14 void dfs(TreeNode *node, int sum, int curSum, vector<int> a) 15 { 16 if (node == NULL) 17 return; 18 19 if (node->left == NULL && node->right == NULL) 20 { 21 if (curSum + node->val == sum) 22 { 23 a.push_back(node->val); 24 ret.push_back(a); 25 } 26 return; 27 } 28 29 a.push_back(node->val); 30 dfs(node->left, sum, curSum + node->val, a); 31 dfs(node->right, sum, curSum + node->val, a); 32 } 33 34 vector<vector<int> > pathSum(TreeNode *root, int sum) { 35 // Start typing your C/C++ solution below 36 // DO NOT write int main() function 37 ret.clear(); 38 vector<int> a; 39 dfs(root, sum, 0, a); 40 return ret; 41 } 42 };
上面的方法中,采用了递归,代码简单也利于理解,如果要是不采用递归该怎么求解呢?
如果不采用递归,就需要在迭代过程中“回溯”,也就需要保存当前节点左右子节点是否已经遍历过,如果没有遍历,则继续往下遍历,如果都遍历过了,则往其父节点回溯
代码如下:
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 vector<vector<int>> pathSum(TreeNode* root, int sum) { 13 vector<vector<int>> res; 14 vector<int> temp; 15 vector<TreeNode*> myStack;//用vector模拟stack 16 stack<bool> isVisitedLeft;//记录左节点是否访问过 17 stack<bool> isVisitedRight;//记录右节点是否访问过 18 TreeNode *top; 19 int index; 20 int count=0; 21 if(NULL == root) 22 return res; 23 if(root->left == NULL && root->right == NULL) 24 { 25 if(root->val == sum) 26 { 27 temp.push_back(root->val); 28 res.push_back(temp); 29 } 30 31 return res; 32 } 33 myStack.resize(2000); 34 myStack[0] = root; 35 isVisitedLeft.push(false); 36 isVisitedRight.push(false); 37 index=0; 38 count += root->val; 39 while(index>=0) 40 { 41 top = myStack[index]; 42 if(!(isVisitedLeft.top()))//左节点没有被访问 43 { 44 isVisitedLeft.pop(); 45 isVisitedLeft.push(true); 46 if(top->left != NULL) 47 { 48 myStack[index+1]= top->left;//插入左节点 49 isVisitedLeft.push(false);//该节点左右节点都没被访问过 50 isVisitedRight.push(false); 51 index++; 52 count+=top->left->val; 53 } 54 55 56 } 57 else if(!(isVisitedRight.top())) 58 { 59 isVisitedRight.pop(); 60 isVisitedRight.push(true); 61 if(top->right != NULL) 62 { 63 myStack[index+1]= top->right; 64 isVisitedLeft.push(false);//该节点左右节点都没被访问过 65 isVisitedRight.push(false); 66 index++; 67 count+=top->right->val; 68 } 69 70 } 71 else 72 { 73 if(count == sum && top->left == NULL && top->right == NULL) 74 { 75 temp.clear(); 76 //for(int i=0;i<myStack.size();i++)不能这样写 77 for(int i=0;i<=index;i++) 78 { 79 temp.push_back(myStack[i]->val);//这里就知道为啥用vector模拟stack,主要是为了遍历方便,也可以用stack,只不过遍历stack需要逐个出栈 80 } 81 res.push_back(temp); 82 } 83 84 count -=top->val; 85 index--; 86 isVisitedLeft.pop(); 87 isVisitedRight.pop(); 88 89 } 90 } 91 return res; 92 } 93 };
--------------------------------------------------------------------------------分割线--------------------------------------------------------------------------------
114. Flatten Binary Tree to Linked List
题目
分析:
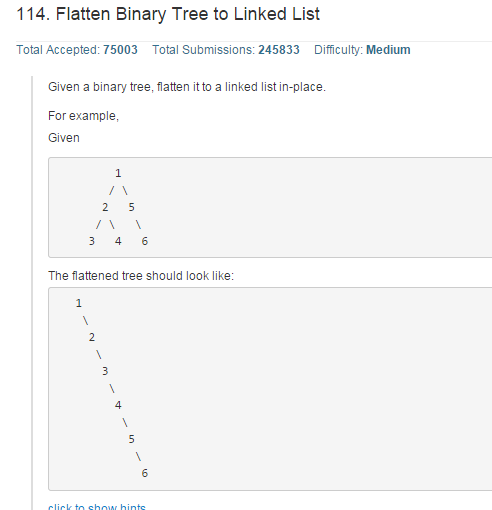
根据题目的例子可以发现,最终得到的结果其实是二叉树前序遍历得到的序列顺序。因此可以仿照前序遍历的递归思想进行操作,代码如下:
代码中有一个lastNode 指针,用于指向当前链表的最后一个节点。
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 TreeNode* lastNode; 13 void flatten(TreeNode* root) { 14 if(NULL == root) 15 return; 16 lastNode = root; 17 preOrder(root); 18 } 19 void preOrder(TreeNode* root) 20 { 21 if(root== NULL) 22 { 23 return ; 24 } 25 TreeNode *temp=NULL; 26 lastNode = root; 27 temp = root->right;//切断右子树,用temp指向右子树 28 root->right = root->left; 29 root->left = NULL; 30 preOrder(root->right); 31 lastNode->right = temp;//右子树的所有节点是lastNode节点之后的 32 preOrder(temp); 33 } 34 };
如果采用非递归的,则需要一个stack,但是不符合题目要求:在本地处理节点(in-place)。


